
| A. | ∠A:∠B:∠C=3:4:5 | B. | ∠A=$\frac{1}{2}$∠B=$\frac{1}{3}$∠C | C. | ∠B=50°,∠C=40° | D. | a=5,b=12,c=13 |
分析 由直角三角形的定义,只要验证最大角是否是90°;由勾股定理的逆定理,只要验证两小边的平方和是否等于最长边的平方即可.
解答 解:A、∵∠A:∠B:∠C=3:4:5,∴∠C=$\frac{5}{12}$180°=75°,故不能判定△ABC是直角三角形;
B、∵∠A=$\frac{1}{2}$∠B=$\frac{1}{3}$∠C,∴∠C=90°,故能判定△ABC是直角三角形;
C、∵∠∠B=50°,∠C=40°,∴∠A=90°,故能判定△ABC是直角三角形;
D、∵a=5,b=12,c=13,∴a2+b2=c2,故能判定△ABC是直角三角形.
故选A.
点评 本题主要考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1>y2>y3 | B. | y3>y2>y1 | C. | y1>y3>y2 | D. | y2>y3>y1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,∠B=40°,∠C=50°,AD平分∠BAC,交BC于D,DE∥AB,交AC于E,则∠ADE的大小是( )
如图,在△ABC中,∠B=40°,∠C=50°,AD平分∠BAC,交BC于D,DE∥AB,交AC于E,则∠ADE的大小是( )| A. | 40° | B. | 45° | C. | 50° | D. | 90° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
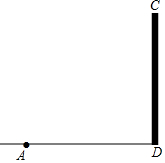 小明同学去大埋旅游时看见一座占塔,他在父母帮助下测得一些数据,首先在地面上的A点测得塔C的仰角为30°,然后沿着向塔的方向前进10m到达B点(点B在线段AD上),则B点测得塔顶C的仰角为45°,请你在图中补画示意图,并求出塔高(精确到0.1m)
小明同学去大埋旅游时看见一座占塔,他在父母帮助下测得一些数据,首先在地面上的A点测得塔C的仰角为30°,然后沿着向塔的方向前进10m到达B点(点B在线段AD上),则B点测得塔顶C的仰角为45°,请你在图中补画示意图,并求出塔高(精确到0.1m)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
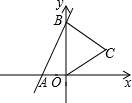 如图,直线y=x+2与x轴、y轴分别交于A,B两点,以OB为边在y轴的右侧作等边三角形OBC.
如图,直线y=x+2与x轴、y轴分别交于A,B两点,以OB为边在y轴的右侧作等边三角形OBC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com