

|
| EC2-BC2 |
| 62-42 |
| 5 |
| 5 |
|
| EC2-BC2 |
| 5 |
| 1 |
| 2 |
| 5 |
| 1 |
| 2 |
| 5 |


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:初中数学 来源: 题型:
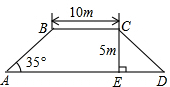 如图,某堤坝横断面为梯形ABCD,若斜坡AB的坡角∠BAD为35゜,斜坡CD的坡度为i=1:1.2(垂直高度CE与水平宽度DE的比),上底BC=10m,堤坝高度CE=5m,求下底AD的长度?(结果精确到0.1m,参考数据:sin35゜≈0.57,cos 35゜≈0.82,tan35゜≈0.70)
如图,某堤坝横断面为梯形ABCD,若斜坡AB的坡角∠BAD为35゜,斜坡CD的坡度为i=1:1.2(垂直高度CE与水平宽度DE的比),上底BC=10m,堤坝高度CE=5m,求下底AD的长度?(结果精确到0.1m,参考数据:sin35゜≈0.57,cos 35゜≈0.82,tan35゜≈0.70)查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
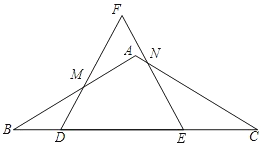 如图,在△ABC中,AB=AC,∠B=30°,BC=8,D在边BC上,E在线段DC上,DE=4,△DEF是等边三角形,边DF交边AB于点M,边EF交边AC于点N.
如图,在△ABC中,AB=AC,∠B=30°,BC=8,D在边BC上,E在线段DC上,DE=4,△DEF是等边三角形,边DF交边AB于点M,边EF交边AC于点N.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,点G是△ABC的重心,CG的延长线交AB于点D,GA=10,GC=8,GB=6,将△ADG绕点D顺时针方向旋转180°得到△BDE,则△EBC的面积为
如图,点G是△ABC的重心,CG的延长线交AB于点D,GA=10,GC=8,GB=6,将△ADG绕点D顺时针方向旋转180°得到△BDE,则△EBC的面积为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com