
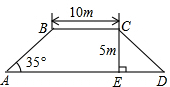
 如图,某堤坝横断面为梯形ABCD,若斜坡AB的坡角∠BAD为35゜,斜坡CD的坡度为i=1:1.2(垂直高度CE与水平宽度DE的比),上底BC=10m,堤坝高度CE=5m,求下底AD的长度?(结果精确到0.1m,参考数据:sin35゜≈0.57,cos 35゜≈0.82,tan35゜≈0.70)
如图,某堤坝横断面为梯形ABCD,若斜坡AB的坡角∠BAD为35゜,斜坡CD的坡度为i=1:1.2(垂直高度CE与水平宽度DE的比),上底BC=10m,堤坝高度CE=5m,求下底AD的长度?(结果精确到0.1m,参考数据:sin35゜≈0.57,cos 35゜≈0.82,tan35゜≈0.70)
| BF |
| AF |
| BF |
| tan35° |
| 5 |
| 0.70 |
| CE |
| ED |
| 1 |
| 1.2 |


 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
| 时间段 | 频数 | 频率 |
| 29分钟及以下 | 108 | 0.54 |
| 30-39分钟 | 24 | 0.12 |
| 40-49分钟 | m | 0.15 |
| 50-59分钟 | 18 | 0.09 |
| 1小时及以上 | 20 | 0.1 |
查看答案和解析>>
科目:初中数学 来源: 题型:
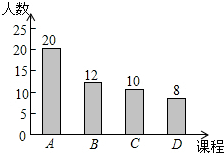 某学校计划开设A、B、C、D四门校本课程供全体学生选修,规定每人必须并且只能选修其中一门,为了了解各部门课程的选修人数.现从全体学生中随机抽取了部分学生进行调查,并把调查结果绘制成如图所示的条形统计图.已知该校全体学生人数为1200名,由此可以估计选修C课程的学生有
某学校计划开设A、B、C、D四门校本课程供全体学生选修,规定每人必须并且只能选修其中一门,为了了解各部门课程的选修人数.现从全体学生中随机抽取了部分学生进行调查,并把调查结果绘制成如图所示的条形统计图.已知该校全体学生人数为1200名,由此可以估计选修C课程的学生有查看答案和解析>>
科目:初中数学 来源: 题型:
| 7 |
| 8 |

查看答案和解析>>
科目:初中数学 来源: 题型:
 随着人民生活水平的提高,购买老年代步车的人越来越多.这些老年代步车却成为交通安全的一大隐患.针对这种现象,某校数学兴趣小组在《老年代步车现象的调查报告》中就“你认为对老年代步车最有效的管理措施”随机对某社区部分居民进行了问卷调查,其中调查问卷设置以下选项(只选一项):
随着人民生活水平的提高,购买老年代步车的人越来越多.这些老年代步车却成为交通安全的一大隐患.针对这种现象,某校数学兴趣小组在《老年代步车现象的调查报告》中就“你认为对老年代步车最有效的管理措施”随机对某社区部分居民进行了问卷调查,其中调查问卷设置以下选项(只选一项):| 管理措施 | 回答人数 | 百分比 |
| A | 25 | 5% |
| B | 100 | m |
| C | 75 | 15% |
| D | n | 35% |
| E | 125 | 25% |
| 合计 | a | 100% |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com