
| 1 |
| 2 |
| 27 |
| 3 |
| a2-b2 |
| a2-ab |
| 2ab+b2 |
| a |
科目:初中数学 来源: 题型:
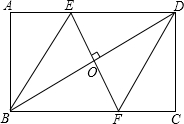 如图,在矩形ABCD中,边AB的长为3,点E,F分别在AD,BC上,连接BE,DF,EF,BD.若四边形BEDF是菱形,且EF=AE+FC,则边BC的长为( )
如图,在矩形ABCD中,边AB的长为3,点E,F分别在AD,BC上,连接BE,DF,EF,BD.若四边形BEDF是菱形,且EF=AE+FC,则边BC的长为( )A、2
| ||||
B、3
| ||||
C、6
| ||||
D、
|
查看答案和解析>>
科目:初中数学 来源: 题型:
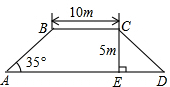 如图,某堤坝横断面为梯形ABCD,若斜坡AB的坡角∠BAD为35゜,斜坡CD的坡度为i=1:1.2(垂直高度CE与水平宽度DE的比),上底BC=10m,堤坝高度CE=5m,求下底AD的长度?(结果精确到0.1m,参考数据:sin35゜≈0.57,cos 35゜≈0.82,tan35゜≈0.70)
如图,某堤坝横断面为梯形ABCD,若斜坡AB的坡角∠BAD为35゜,斜坡CD的坡度为i=1:1.2(垂直高度CE与水平宽度DE的比),上底BC=10m,堤坝高度CE=5m,求下底AD的长度?(结果精确到0.1m,参考数据:sin35゜≈0.57,cos 35゜≈0.82,tan35゜≈0.70)查看答案和解析>>
科目:初中数学 来源: 题型:
| 在 |
| • |
| (1) |
| • |
| 的 |
| • |
| 条 |
| • |
| 件 |
| • |
| 下 |
| • |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
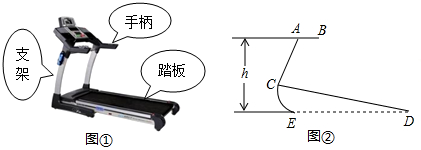
 为提高居民的节水意识,向阳小区开展了“建设节水型社区,保障用水安全”为主题的节水宣传活动,小莹同学积极参与小区的宣传活动,并对小区300户家庭用水情况进行了抽样调查,他在300户家庭中,随机调查了50户家庭5月份的用水量情况,结果如图所示.
为提高居民的节水意识,向阳小区开展了“建设节水型社区,保障用水安全”为主题的节水宣传活动,小莹同学积极参与小区的宣传活动,并对小区300户家庭用水情况进行了抽样调查,他在300户家庭中,随机调查了50户家庭5月份的用水量情况,结果如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com