
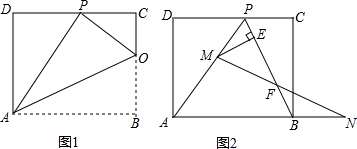
| 在 |
| • |
| (1) |
| • |
| 的 |
| • |
| 条 |
| • |
| 件 |
| • |
| 下 |
| • |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| OC |
| PD |
| OP |
| PA |
| CP |
| DA |
|
| 1 |
| 2 |
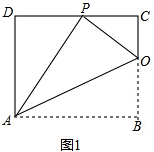
| 1 |
| 2 |
| 1 |
| 2 |
| DP |
| AP |
| 1 |
| 2 |
| 1 |
| 2 |
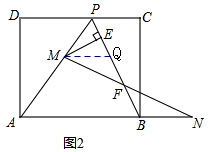
|
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 82+42 |
| 5 |
| 1 |
| 2 |
| 5 |
| 5 |


科目:初中数学 来源: 题型:
A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:初中数学 来源: 题型:
 随着人民生活水平的提高,购买老年代步车的人越来越多.这些老年代步车却成为交通安全的一大隐患.针对这种现象,某校数学兴趣小组在《老年代步车现象的调查报告》中就“你认为对老年代步车最有效的管理措施”随机对某社区部分居民进行了问卷调查,其中调查问卷设置以下选项(只选一项):
随着人民生活水平的提高,购买老年代步车的人越来越多.这些老年代步车却成为交通安全的一大隐患.针对这种现象,某校数学兴趣小组在《老年代步车现象的调查报告》中就“你认为对老年代步车最有效的管理措施”随机对某社区部分居民进行了问卷调查,其中调查问卷设置以下选项(只选一项):| 管理措施 | 回答人数 | 百分比 |
| A | 25 | 5% |
| B | 100 | m |
| C | 75 | 15% |
| D | n | 35% |
| E | 125 | 25% |
| 合计 | a | 100% |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 2 |
| 2 |
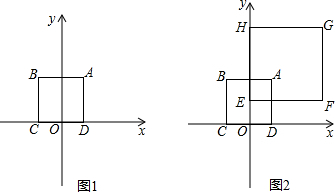
查看答案和解析>>
科目:初中数学 来源: 题型:
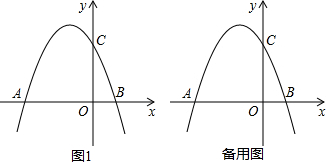
查看答案和解析>>
科目:初中数学 来源: 题型:
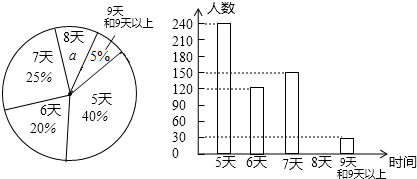
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com