
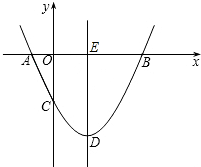
 如图,抛物线y=
如图,抛物线y=| 1 |
| 2 |
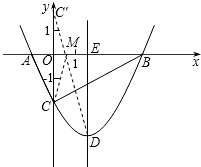 解:∵点A(-1,0)在抛物线y=
解:∵点A(-1,0)在抛物线y=| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 25 |
| 8 |
| OM |
| EM |
| OC′ |
| ED |
| m | ||
|
| 2 | ||
|
| 24 |
| 41 |
| 24 |
| 41 |


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:初中数学 来源: 题型:
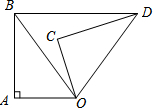 如图,在△OAB中,∠A=90°,△OCD是把△OAB以O为旋转中心,顺时针旋转而得到的(其中C与A对应),记旋转角为α,∠OBA为β.
如图,在△OAB中,∠A=90°,△OCD是把△OAB以O为旋转中心,顺时针旋转而得到的(其中C与A对应),记旋转角为α,∠OBA为β.查看答案和解析>>
科目:初中数学 来源: 题型:
| A-C | C-D | E-D | F-E | G-F | B-G |
| 90米 | 80米 | -60米 | 50米 | -70米 | 40米 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,下列说法中正确的是( )
如图,下列说法中正确的是( )| A、OA的方向是西偏北26°48' |
| B、OA的方向是北偏西63°12' |
| C、OA的方向是北偏西26°48' |
| D、OA的方向是北偏西26°88' |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com