
【题目】如图,在边长为4的正方形ABCD中,点E是边CD的中点,AE的垂直平分线交边BC于点G,交边AE于点F,连接DF,EG,以下结论:①DF= ![]() ,②DF∥EG,③△EFG≌△ECG,④BG=
,②DF∥EG,③△EFG≌△ECG,④BG= ![]() ,正确的有:(填写序号)
,正确的有:(填写序号)
【答案】①④
【解析】解:如图,设FG交AD于M,连接BE.
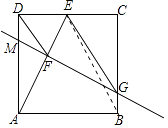
∵四边形ABCD是正方形,
∴AB=BC=CD=AD=4,∠ADC=∠C=90°,
∵DE=EC=2,
在Rt△ADE中,AE= ![]() =
= ![]() =2
=2 ![]() .
.
∵AF=EF,
∴DF= ![]() AE=
AE= ![]() ,故①正确,
,故①正确,
易证△AED≌△BEC,
∴∠AED=∠BEC,
∵DF=EF,
∴∠FDE=∠FED=∠BEC,
∴DF∥BE,
∵BE与EG相交,
∴DF与EG不平行,故②错误,
∵AE⊥MG,易证AE=MG=2 ![]() ,
,
由△AFM∽△ADE,可知 ![]() =
= ![]() ,
,
∴FM= ![]() ,FG=
,FG= ![]() ,
,
在Rt△EFG中,EG= ![]() =
= ![]() ,
,
在Rt△ECG中,CG= ![]() =
= ![]() ,
,
∴BG=BC﹣CG=4﹣ ![]() =
= ![]() ,故④正确,
,故④正确,
∵EF≠EC,FG≠CG,∴△EGF与△EGC不全等,故③错误,
所以答案是①④.
【考点精析】利用线段垂直平分线的性质和正方形的性质对题目进行判断即可得到答案,需要熟知垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】第八届中国(深圳)文博会以总成交额143 300 000 000元再创新高,将数143 300 000 000用科学记数法表示为( )
A.1.433×1010
B.1.433×1011
C.1.433×1012
D.0.1433×1012
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F.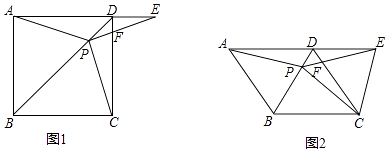
(1)求证:PC=PE;
(2)图1中与∠EAP相等的角是和 , 则可求∠CPE=°;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°,连接CE,请直接写出∠CPE=°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解八年级学生的视力情况,对八年级的学生进行了一次视力调查,并将调查数据进行统计整理,绘制出如下频数分布表和频数分布直方图的一部分.
视力 | 频数(人) | 频率 |
4.0≤x<4.3 | 20 | 0.1 |
4.3≤x<4.6 | 40 | 0.2 |
4.6≤x<4.9 | 70 | 0.35 |
4.9≤x<5.2 | a | 0.3 |
5.2≤x<5.5 | 10 | b |
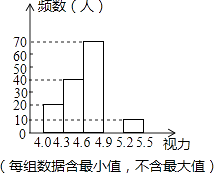
(1)在频数分布表中,a= , b=;
(2)将频数分布直方图补充完整;
(3)若视力在4.6以上(含4.6)均属正常,求视力正常的人数占被调查人数的百分比是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系中的位置如图所示,△ABC的顶点均在格点上,其中每个小正方形的边长为1个单位长度,将△ABC绕原点O旋转180°得△A1B1C1 . 
(1)在图中画出△A1B1C1;
(2)写出点A1的坐标;
(3)求出点C所经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题8分)为培养学生数学学习兴趣,某校七年级准备开设“神奇魔方”、“魅力数独”、“数学故事”、“趣题巧解”四门选修课(每位学生必须且只选其中一门).
(1)学校对七年级部分学生进行选课调查,得到如图所示的统计图,根据该统计图,请估计该校七年级480名学生选“数学故事”的人数。
(2)学校将选“数学故事”的学生分成人数相等的A,B,C三个班,小聪、小慧都选择了“数学故事”,已知小聪不在A班,求他和小慧被分到同一个班的概率.(要求列表或画树状图)
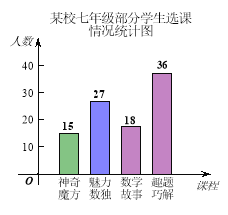
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com