
【题目】如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F.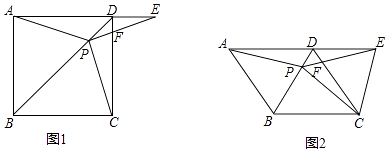
(1)求证:PC=PE;
(2)图1中与∠EAP相等的角是和 , 则可求∠CPE=°;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°,连接CE,请直接写出∠CPE=°.
【答案】
(1)证明:∵四边形ABCD为正方形,
∴BA=BC,∠ABD=∠CBD=45°,
在△ABP和△CBP中
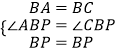 ,
,
∴△ABP≌△CBP,
∴PA=PC,
∵PA=PE,
∴PC=PE;
(2)∠E,∠PCD,90
(3)60
【解析】(2)解:∵△ABP≌△CBP,
∴∠PAB=∠PCB,
∴∠PAD=∠PCD,
∵PA=PE,
∴∠PAE=∠E,
∴∠PCD=∠E,
而∠DFE=∠PFC,
∴∠CPF=∠EDF=90°,
即图1中与∠EAP相等的角是∠E和∠PCD;
⑶∵四边形ABCD为菱形,
∴BA=BC,∠ABD=∠CBD=60°,∠ADC=∠ABC=120°,
∴∠EDC=60°,
在△ABP和△CBP中
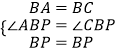 ,
,
∴△ABP≌△CBP,
∴PA=PC,∠PAB=∠PCB,
∴∠PAD=∠PCD,
∵PA=PE,
∴∠PAD=∠PED,
∴∠PCD=∠PED,
而∠DFE=∠PFC,
∴∠CPF=∠EDF=60°.
故答案为∠E,∠PCD,90,60.
(1)四边形ABCD为正方形,得到BA=BC,∠ABD=∠CBD=45°,△ABP≌△CBP,得到PA=PC,由PA=PE,得到PC=PE;(2)由△ABP≌△CBP,得到∠PAB=∠PCB,∠PAD=∠PCD,由PA=PE,得到∠PAE=∠E,∠PCD=∠E,而∠DFE=∠PFC,得到∠CPF=∠EDF=90°,即图1中与∠EAP相等的角是∠E和∠PCD;⑶由四边形ABCD为菱形,得到BA=BC,∠ABD=∠CBD=60°,∠ADC=∠ABC=120°,∠EDC=60°,△ABP≌△CBP,得到PA=PC,∠PAB=∠PCB,∠PAD=∠PCD,由PA=PE,得到∠PAD=∠PED,∠PCD=∠PED,而∠DFE=∠PFC,得到∠CPF=∠EDF=60°;故答案为∠E,∠PCD,90,60.


科目:初中数学 来源: 题型:
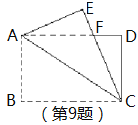
【题目】如图,矩形纸片ABCD中,AB=4,BC=6,将△ABC沿AC折叠,使点B落在点E处,CE交AD于点F,则DF的长等于
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学习了统计知识后,小明就本班同学的上学方式进行了一次调查统计,图(1)和图(2)是他通过采集数据后,绘制的两幅不完整的统计图.请你根据图中提供的信息,解答以下问题: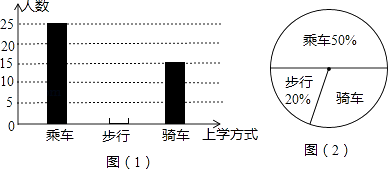
(1)求该班共有多少名学生;
(2)求出该班“步行”的人数并在图(1)中,将表示“步行”的部分补充完整;
(3)如果小明所在年级共计600人,请你根据样本数据,估计一下该年级步行上学的学生人数是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为4的正方形ABCD中,点E是边CD的中点,AE的垂直平分线交边BC于点G,交边AE于点F,连接DF,EG,以下结论:①DF= ![]() ,②DF∥EG,③△EFG≌△ECG,④BG=
,②DF∥EG,③△EFG≌△ECG,④BG= ![]() ,正确的有:(填写序号)
,正确的有:(填写序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司的年销售额为a元,成本为销售额的60%,税额和其他费用合计为销售额的P%.
(1)用关于a、P的代数式表示该公司的年利润;
(2)若a=8000万,P=7,则该公司的年利润为多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com