
| A. |  | B. |  | C. | 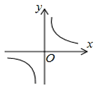 | D. | 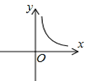 |
科目:初中数学 来源: 题型:解答题
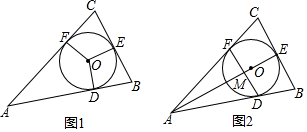
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
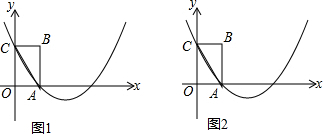
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
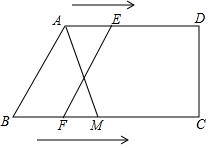 在四边形ABCD中,AD∥BC,BC⊥CD,AD=6cm,BC=10cm,点E从A出发以1cm/s的速度向D运动,点F从点B出发,以2cm/s的速度向点C运动,当其中一点到达终点,而另一点也随之停止,设运动时间为t,
在四边形ABCD中,AD∥BC,BC⊥CD,AD=6cm,BC=10cm,点E从A出发以1cm/s的速度向D运动,点F从点B出发,以2cm/s的速度向点C运动,当其中一点到达终点,而另一点也随之停止,设运动时间为t,查看答案和解析>>
科目:初中数学 来源: 题型:填空题
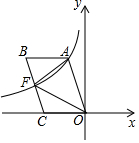 如图,四边形OABC是平行四边形,边OC在x轴的负半轴上,反比例y=$\frac{k}{x}$(k<0)的图象经过点A与BC的中点F,连接AF、OF,若△AOF的面积为9,则k的值为-9.
如图,四边形OABC是平行四边形,边OC在x轴的负半轴上,反比例y=$\frac{k}{x}$(k<0)的图象经过点A与BC的中点F,连接AF、OF,若△AOF的面积为9,则k的值为-9.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
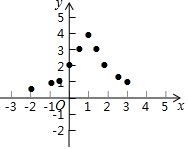 小东根据学习函数的经验,对函数y=$\frac{4}{{(x-1)}^{2}+1}$的图象与性质进行了探究.下面是小东的探究过程,请补充完整,并解决相关问题:
小东根据学习函数的经验,对函数y=$\frac{4}{{(x-1)}^{2}+1}$的图象与性质进行了探究.下面是小东的探究过程,请补充完整,并解决相关问题:| x | … | -2 | -1 | -$\frac{1}{2}$ | 0 | $\frac{1}{2}$ | 1 | $\frac{3}{2}$ | 2 | $\frac{5}{2}$ | 3 | 4 | … |
| y | … | $\frac{2}{5}$ | $\frac{4}{5}$ | $\frac{16}{13}$ | 2 | $\frac{16}{5}$ | 4 | $\frac{16}{5}$ | 2 | $\frac{16}{13}$ | $\frac{4}{3}$ | m | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com