练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

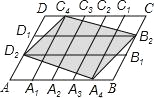
    【题目】在平行四边形ABCD中，点A1，A2，A3，A4和C1，C2，C3，C4分别AB和CD的五等分点，点B1，B2和D1，D2分别是BC和DA的三等分点，已知四边形A4B2C4D2的面积为1，则平行四边形ABCD面积为（　　）

    A. 2 B. C. D. 15

    【答案】C

    【解析】设平行四边形ABCD的面积是S，设AB=5a，BC=3b．AB边上的高是3x，BC边上的高是5y．
    则S=5a3x=3b5y．即ax=by=．
    △AA4D2与△B2CC4全等，B2C=BC=b，B2C边上的高是4y．
    则△AA4D2和△B2CC4的面积是2by= ．
    同理△D2C4D与△A4BB2的面积是．
    则四边形A4B2C4D2的面积是=1，
    解得S=．
    故选C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在 ABCD中，∠DAB＝60°，点E，F分别在CD，AB的延长线上，且AE＝AD，CF＝CB．

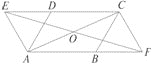
    （1）求证：四边形AFCE是平行四边形．

    （2）若去掉已知条件的“∠DAB＝60°，上述的结论还成立吗 ”若成立，请写出证明过程；若不成立，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】把下列各数填在相应的集合里：

    2018，1，－1，－2014，0.5，，－，－0.75，0，20%，

    整数集合：{____________________…}；正分数集合：{________________…}；

    负分数集合：{________________…}；正数集合：{__________________…}；

    负数集合：{__________________…}．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在□ABCD中，对角线AC，BD相交于点O，AE⊥BD于点E，CF⊥BD于点F，连结AF，CE，则下列结论：①CF=AE；②OE=OF；③DE=BF；④图中共有四对全等三角形.其中正确结论的个数是（ ）

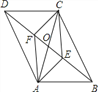
    A. 4 B. 3 C. 2 D. 1

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某市甲、乙两个汽车销售公司，去年一至十月份每月销售同种品牌汽车的情况如图所示：

    （1）请你根据左图填写右表：

    销售公司

    平均数

    方差

    中位数

    众数

    甲

    9

    乙

    9

    17.0

    8

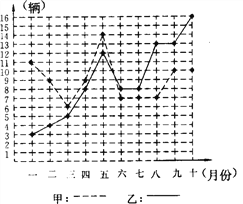
    （2）请你从以下两个不同的方面对甲、乙两个汽车销售公司去年一至十月份的销售情况进行分析：

    ①从平均数和方差结合看；

    ②从折线图上甲、乙两个汽车销售公司销售数量的趋势

    看（分析哪个汽车销售公司较有潜力）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在矩形ABCD中，BC=5，AB=3，分别经过点B和点D的两个动圆均与AC相切，且与AB、BC、AD、DC分别交于点G、H、E、F，则EF+GH的最小值是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一家公司招考员工，每位考生要在A，B，C，D，E这5道试题中谁家抽出2道题回答，规定答对其中1题即为合格．
    （1）请用树状图表示出所有可能的出题情形；
    （2）已知某位考生只会答A，B两题，试求这位考生合格的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某制造企业有一座对生产设备进行水循环冷却的冷却塔，冷却塔的顶部有一个进水口，3小时恰好可以注满这座空塔，底部有一个出水口，7小时恰好可以放完满塔的水．为了保证安全，塔内剩余水量不得少于全塔水量的 ，出水口一直打开，保证水的循环，进水口根据水位情况定时对冷却塔进行补水．假设每次恰好在剩余水量为满水量的m倍时开始补水，补满后关闭进水口．
    （1）当m= 时，请问：两次补水之间相隔多长时间？每次补水需要多长时间？
    （2）能否找到适当的m值，使得两次补水的间隔时间和每次的补水时间一样长？如果能，请求出m值；如果不能，请你分析两次补水的间隔时间和每次的补水时间之间的数量关系，并表示出来．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在已知的ABC中，按以下步骤作图：
    ①分别以B，C为圆心，以大于 BC的长为半径作弧，两弧相交于两点M，N；
    ②作直线MN交AB于点D，连接CD.若CD=AC，∠A=50°，则∠ACB的度数为（ ）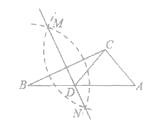

    A.90°
    B.95°
    C.100°
    D.105°

    查看答案和解析>>

    同步练习册答案