
【题目】我们在探究一元二次方程根与系数的关系中发现:如果关于x的方程x2+px+q=0的两个根是x1,x2,那么由求根公式可推出x1+x2=﹣p,x1x2=q,请根据这一结论,解决下列问题:
(1)若α,p是方程x2﹣3x+1=0的两根,则α+β= ,αβ= ;若2,3是方程x2+mx+n=0的两根,则m= ,n= ;
(2)已知a,b满足a2﹣5a+3=0,b2﹣5b+3=0,求![]() 的值;
的值;
(3)已知a,b,c满足a+b+c=0,abc=5,求正整数c的最小值,
【答案】(1)3,1,-5,6;(2)![]() 或2;(3)3
或2;(3)3
【解析】
(1)根据根与系数的关系即可得到结论;
(2)根据α,b满足a2-5a+3=0,b2-5b+3=0,得到α,b是方程x2-5x+3=0的解.当α≠b时,是方程a+b=5,ab=3,根据根与系数的关系即可得到结论;当α=b时,原式=2;
(3)根据a+b+c=0,abc=5,求得a+b=-c,ab=![]() ,于是得到α,b是方程x2-
,于是得到α,b是方程x2-![]() =0的解,即可得到结论.
=0的解,即可得到结论.
(1)α,p是方程x2-3x+1=0的两根,则α+β=3,αβ=1;若2,3是方程x2+mx+n=0的两根,则m=-5,n=6;
故答案为:3,1,-5,6;
(2)∵α,b满足a2-5a+3=0,b2-5b+3=0,
∴α,b是方程x2-5x+3=0的解.
当α≠b时,是方程a+b=5,ab=3,
∴![]() ,
,
当α=b时,原式=2;
(3)∵a+b+c=0,abc=5,
∴a+b=-c,ab=![]() ,
,
∴α,b是方程x2-cx+![]() =0的解,
=0的解,
∴c2-4×![]() ≥0,
≥0,
∵c是正整数,
∴c3-20≥0,即c≥![]() .
.
∴正整数c的最小值是3.
∴正整数c的最小值是3.


科目:初中数学 来源: 题型:
【题目】为了解某校九年级男生1000米跑的水平,从中随机抽取部分男生进行测试,并把测试成绩分为D、C、B、A四个等次绘制成如图所示的不完整的统计图,请你依图解答下列问题:
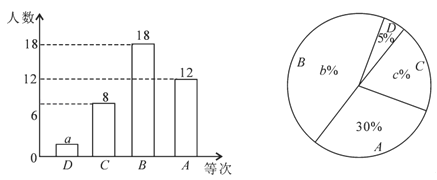
(1)a= ,b= ,c= ;
(2)扇形统计图中表示C等次的扇形所对的圆心角的度数为 度;
(3)学校决定从A等次的甲、乙、丙、丁四名男生中,随机选取两名男生参加全市中学生1000米跑比赛,请用列表法或画树状图法,求甲、乙两名男生同时被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水渠的横截面呈抛物线,水面的宽度为AB(单位:米),现以AB所在直线为x轴,以抛物线的对称轴为y轴建立如图所示的平面直角坐标系,设坐标原点为O.已知AB=8米,设抛物线解析式为y=ax2﹣4.
(1)求a的值;
(2)点C(﹣1,m)是抛物线上一点,点C关于原点O的对称点为点D,连接CD,BC,BD,求△BCD的面积.
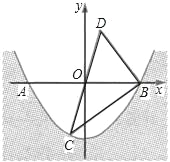
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ABC直角三角形,延长AB到D,使BD=BC,在BC上取BE=AB,连接DE.△ABC顺时针旋转后能与△EBD重合,那么:
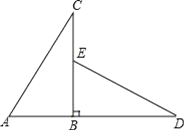
(1)旋转中心是哪一点?旋转角是多少度?
(2)AC与DE的关系怎样?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABC的三个顶点A,B,C都在格点上.将△ABC绕点A按顺时针方向旋转90°得到△AB′C′.
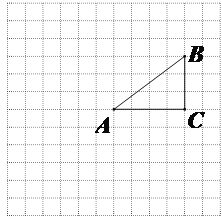
(1)在正方形网格中,画出△AB′C′;
(2)计算线段AB在变换到AB′的过程中扫过的区域的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c与x轴交于A(﹣1,0)和B(3,0)两点,交y轴于点E.
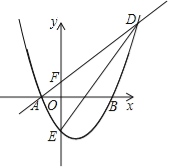
(1)求此抛物线的解析式.
(2)若直线y=x+1与抛物线交于A、D两点,与y轴交于点F,连接DE,求△DEF的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com