
| 9 |
| 2 |
| 9 |
| 2 |

| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 8 |
| 9 |
| 2 |
 (3)设CO=xkm,则OD=(80-x)km.
(3)设CO=xkm,则OD=(80-x)km.| 9 |
| 2 |


科目:初中数学 来源: 题型:
| 3 | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
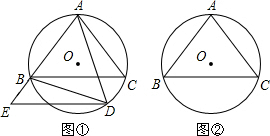 E交直线AB于点E,连接BD.
E交直线AB于点E,连接BD.查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 2 |

| 12 |
| 5 |
| 12 |
| 5 |

查看答案和解析>>
科目:初中数学 来源:2012年浙教版初中数学八年级下 5.6三角形的中位线练习卷(解析版) 题型:解答题
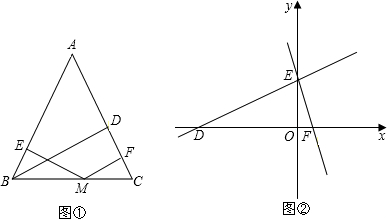
某厂有一块如图所示的△ABC铁板,根据需要,现要把它加工成一个平行四边形铁板.要把材料完全利用起来,可怎样加工?请你利用学过的知识帮助工人师傅把切割的线用虚线画出来,并指出加工后的平行四边形.能否将此三角形铁板加工成长方形?请予以探索.



查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com