
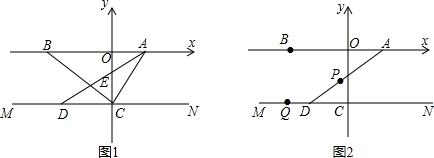
���� ��1�����ݷǸ������������a��b��c��ֵ��Ȼ����������������ʽ��⣻
��2����ȷ��D�����꣬�����ô���ϵ�������ֱ��AD�Ľ���ʽ��Ȼ������Ա���Ϊ0�ĺ���ֵ���ɵõ�E�����ꣻ
��3���������⻭������ͼ�Σ����PQM=2��������ƽ���ߵ����ʿɼ������APQ=360��-��BAP-��PQM=325��-2�����ٸ��ݽ�ƽ���߶���õ���PQG=$\frac{1}{2}$��PQM=������APH=��QPH=$\frac{1}{2}$��APQ=$\frac{325��}{2}$-��������ƽ���ߵ����ʿɱ�ʾ����QPF=180��-��PQG=180��-�������HPF=��QPF-��QPH=$\frac{35��}{2}$�����ϡ�ADN=��BAD=35�㣬���ǿɼ����$\frac{��HPF}{��ADN}$=$\frac{1}{2}$��ͬ���ɵá�HPF��=180��-��HPF=$\frac{325��}{2}$����$\frac{��HPF��}{��ADN}$=$\frac{65}{14}$��
��� �⣺��1����|a-2|+|b+4|+$\sqrt{c+3}$=0��
��a=2��b=-4��c=-3��
���ABC�����=$\frac{1}{2}$��3����2+4��=9��
��2����MN��x�ᣬC��0��-3����
��D��-3��-3����
��AD�Ľ���ʽΪy=mx+n��
��A��2��0����D��-3��-3���ֱ�����$\left\{\begin{array}{l}{2m+n=0}\\{-3m+n=-3}\end{array}\right.$�����$\left\{\begin{array}{l}{m=\frac{3}{5}}\\{n=-\frac{6}{5}}\end{array}\right.$��
��ֱ��AD�Ľ���ʽΪy=$\frac{3}{5}$x-$\frac{6}{5}$��
��x=0ʱ��y=$\frac{3}{5}$x-$\frac{6}{5}$=-$\frac{6}{5}$��
��E��������0��-$\frac{6}{5}$����
��3��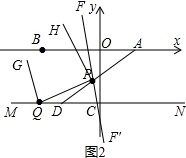 ��ͼ�����PQM=2����
��ͼ�����PQM=2����
��MN��AB��
���APQ=360��-��BAP-��PQM=360��-35��-2��=325��-2����
������QGƽ����PQM������PHƽ�֡�APQ��
���PQG=$\frac{1}{2}$��PQM=������APH=��QPH=$\frac{1}{2}$��APQ=$\frac{325��}{2}$-����
��PF��QG��
���QPF=180��-��PQG=180��-����
���HPF=��QPF-��QPH=180��-��-��$\frac{325��}{2}$-����=$\frac{35��}{2}$��
��MN��AB��
���ADN=��BAD=35�㣬
��$\frac{��HPF}{��ADN}$=$\frac{1}{2}$��
ͬ���ɵá�HPF��=180��-��HPF=180��-$\frac{35��}{2}$=$\frac{325��}{2}$��
��$\frac{��HPF��}{��ADN}$=$\frac{\frac{325��}{2}}{35��}$=$\frac{65}{14}$��
��$\frac{��HPF}{��ADN}$��ֵΪ$\frac{1}{2}$��$\frac{65}{14}$��
���� ���⿼����������ͼ�����ʣ����õ�����������Ӧ�߶εij����ж��߶����������λ�ù�ϵ��Ҳ������ƽ���ߵ����ʣ���Ӧ��3��ͨ�����PQM=2����ʹ�����йصĽ����ױ�ʾ��


 ���Ǽ���С����ϵ�д�
���Ǽ���С����ϵ�д� �Ͻ�ƽ���Ȿϵ�д�
�Ͻ�ƽ���Ȿϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
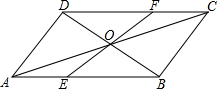 E��F�ֱ���?ABCD�ı�AB��CD�ϵ�һ�㣬��DF=BE��O��BD���е㣬EF����O����֤��EF��AC����ƽ�֣�
E��F�ֱ���?ABCD�ı�AB��CD�ϵ�һ�㣬��DF=BE��O��BD���е㣬EF����O����֤��EF��AC����ƽ�֣��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -1 | B�� | 0 | C�� | 3 | D�� | $\sqrt{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com