Question

1．某商店今年1-6月份经营A、B两种电子产品，已知A产品每个月的销售数量y（件）与月份x（1≤x≤6且x为整数）之间的关系如表今年1-6月份经营A、B两种电子产品，已知A产品 每个月的销售数量y（件）与月份x（1≤x≤6且x为整数）之间的关系如表

x	1	2	3	4	5	6
y	600	300	200	150	120	100

A产品每个月的售价z（元）与月份x之间的函数关系式为：z=10x，已知B产品每个月的销售数量m（件）与月份x之间的关系为：m=-2x+62，B产品每个月的售价n（元）与月份x存在如图所示的变化趋势．
（1）请观察题中表格，用所学过的一次函数或反比例函数的有关知识，直接写出y与x的函数关系式
（2）请观察如图所示的变化趋势，求出n与x的函数关系式
（3）求出此商店1-6月份经营A、B两种电子产品的销售总额w与月份x之间的函数关系式
（4）今年7月份，商店调整了A、B两种电子产品产品的价格，A产品价格在6月份基础上增加a%，B产品价格在6月份基础上减少a%，结果7月份A产品的销售数量比6月份减少2a%，B产品的销售数量比6月份增加2a%，若调整价格后7月份的销售总额比6月份的销售总额少2000元，请根据以下参考数据估算a的值．（参考数据：6.3²=39.69，6.4²=40.91，6.5²=42.25，6.6²=43.56）

Answer 1

分析 （1）根据图表中600×1=600，300×2=600…，得出此函数是反比例函数，k=600，即可得出答案；
（2）由图象可以列出函数解析式，设n=kx+b，代入两点解得k、b，即可得出解析式；
（3）利用销售总额w与y，z，m，n，之间的关系，即可得出月份x之间的函数关系式；
（4）根据6月份A产品的售价以及6月份B产品的售价，得出6月份B产品的销售数量，进而求出a%的值，分析得出a的值．

解答 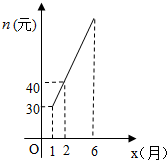解：（1）y=$\frac{600}{x}$；

（2）令n=kx+b（k≠0），
∵n=kx+b（k≠0）过（1，30），（2，40）
∴$\left\{\begin{array}{l}{30=k+b}\\{40=2k+b}\end{array}\right.$，
∴$\left\{\begin{array}{l}{k=10}\\{b=20}\end{array}\right.$，
∴n=10x+20；

（3）利用销售总额w与y，z，mn，之间的关系，即可得出月份x之间的函数关系式；
W=yz+mn=$\frac{600}{x}$•10x+（-2x+62）（10x+20）
=6000+（-20x²+580x+1240），
=-20x²+580x+7240；

（4）今年6月份A产品的售价：z=10×6=60元
今年6月份B产品的售价：n=10×6+20=80元
今年6月份B产品的销售数量：
m=-2×6+62=50件，
60（1+a%）•100（1-2a%）+80（1-a%）•50（1+2a%），
=60×100+50×80-2000，
令p=a%，整理得10p²+p-1=0，
∴p₁=$\frac{-1+\sqrt{41}}{20}$，p₂=$\frac{-1-\sqrt{41}}{20}$（舍去）
∵6.3²=39.69，6.4²=40.91，6.5²=42.25而40.91更接近41，
∴$\sqrt{41}$≈6.4，
∴p$≈\frac{-1+6.4}{20}$，
∴a≈27，
∴a的值约为27．

点评 此题主要考查了二次函数的应用以及待定系数法求一次函数解析式和一元二次方程的解法等知识，运用二次函数解决实际问题是中考中热点题型，同学们应重点掌握．