
【题目】两个大小不同的等腰直角三角形三角板如图①所示放置,图②是由它抽象出的几何图形,B,C,E在同一条直线上,连接DC, 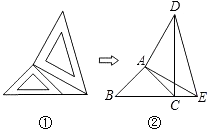
(1)请找出图②中的全等三角形,并给予说明(说明:结论中不得含有未标识的字母);
(2)试说明:DC⊥BE.
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:
【题目】某幼儿园的阿姨给小朋友分苹果,如果每人3个还少3个,如果每人2个又多2个,请问共有多少个小朋友?( )
A. 4个B. 5个C. 10个D. 12个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB>BC,AB=AC,DE是AB的垂直平分线,垂足为D点,交AC于点E. 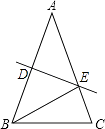
(1)若∠ABE=38°,求∠EBC的度数;
(2)若△ABC的周长为36cm,一边为13cm,求△BCE的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
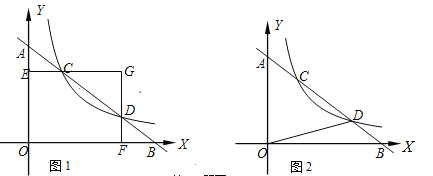
【题目】探究:如图1 ,直线l与坐标轴的正半轴分别交于A,B两点,与反比例函数![]() 的图象交于C,D两点(点C在点D的左边),过点C作CE⊥y轴于点E,过点D作DF⊥x轴于点F,CE与DF交于点G(a,b).
的图象交于C,D两点(点C在点D的左边),过点C作CE⊥y轴于点E,过点D作DF⊥x轴于点F,CE与DF交于点G(a,b).
(1)若![]() ,请用含n的代数式表示
,请用含n的代数式表示![]() ;
;
(2)求证: ![]() ;
;
应用:如图2,直线l与坐标轴的正半轴分别交于点A,B两点,与反比例函数![]() 的图象交于点C,D两点(点C在点D的左边),已知
的图象交于点C,D两点(点C在点D的左边),已知![]() ,△OBD的面积为1,试用含m的代数式表示k.
,△OBD的面积为1,试用含m的代数式表示k.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校食堂的中餐与晚餐的资费标准如下:
种类 | 单价 |
米饭 | 0.5元/份 |
A类套餐菜 | 3.5元/份 |
B类套餐菜 | 2.5元/份 |
小杰同学某星期从周一到周五每天的中餐与晚餐均在学校选用A类或B类中的一份套餐菜与一份米饭用餐,这五天共消费36元.请问小杰在这五天内,A,B类套餐菜各选用了多少次?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分6分)我校学生会发现同学们就餐时剩余饭菜较多,浪费严重,于是准备在校内倡导“光盘行动”,让同学们珍惜粮食,为了让同学们理解这次活动的重要性,校学生会在某天午餐后,随机调查了部分同学这餐饭菜的剩余情况,并将结果统计后绘制成了如图所示的不完整的统计图.

(1)这次被调查的同学共有 名;
(2)把条形统计图补充完整;
(3)校学生会通过数据分析,估计这次被调查的所有学生一餐浪费的食物可以供200人用一餐.据此估算,该校1800名学生一餐浪费的食物可供多少人食用一餐?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知线段AC∥y轴,点B在第一象限,且AO平分∠BAC,AB交y轴与G,连OB、OC. 
(1)判断△AOG的形状,并予以证明;
(2)若点B、C关于y轴对称,求证:AO⊥BO;
(3)在(2)的条件下,如图2,点M为OA上一点,且∠ACM=45°,BM交y轴于P,若点B的坐标为(3,1),求点M的坐标. 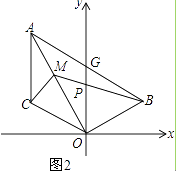
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,点E、D分别从A、C出发,沿AC,CB方向以相同的速度在线段AC,CB上运动,AD、BE相交于F点. 
(1)求证:△ABE≌△CAD;
(2)当E、D运动时,∠BFD大小是否发生改变?若不变求其大小,若改变求其变化范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com