
【题目】在△ABC中,AB>BC,AB=AC,DE是AB的垂直平分线,垂足为D点,交AC于点E. 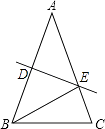
(1)若∠ABE=38°,求∠EBC的度数;
(2)若△ABC的周长为36cm,一边为13cm,求△BCE的周长.
【答案】
(1)解:∵DE是AB的垂直平分线,
∴AE=BE,
∴∠ABE=∠A=38°,
∵AB=AC,
∴∠ABC=∠C= ![]() =71°,
=71°,
∴∠EBC=∠ABC﹣∠ABE=71°﹣38°=33°
(2)解:当BC=13cm时,AB=AC=11.5cm,
∵AE=BE,
∴△BCE的周长为BC+BE+CE=BC+AE+CE=BC+AC=13cm+11.5cm=24.5cm;
当AB=AC=13cm时,则BC=10cm,
∵AE=BE,
∴△BCE的周长为BC+BE+CE=BC+AE+CE=BC+AC=10cm+13cm=23cm;
即△BCE的周长为24.5cm或23cm
【解析】(1)由DE是AB的垂直平分线,根据线段垂直平分线的性质得出AE=BE,则可求得∠ABE的度数,又由AB=AC,根据等边对等角与三角形内角和定理,即可求得∠ABC的度数,继而求得答案;(2)求出AC和BC的值,再根据线段垂直平分线的性质得出AE=BE,求出△BCE的周长=AC+BC,代入求出即可.
【考点精析】根据题目的已知条件,利用线段垂直平分线的性质的相关知识可以得到问题的答案,需要掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等.


 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源: 题型:
【题目】如图所示,每个圆周上的数是按下述规则逐次标出的:第一次先在圆周上标出0,1两个数(如图1);第二次又在第一次标出的两个数之间的圆周上,分别标出这两个数的和(图2);第三次再在第二次标出的所有相邻两数之间的圆周上,分别标出相邻两数的和(如图3).按此规则以此类推,第2013次标完数字后,圆周上所有数字的和S2013= . 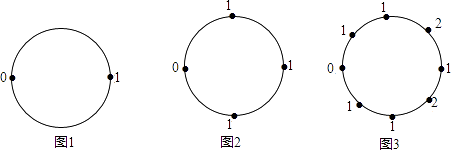
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校校园足球训练队队员的年龄有13、14、15、16四种年龄,统计结果如表:
年龄(岁) | 13 | 14 | 15 | 16 |
人数(个) | 14 | 15 | 16 | 17 |
根据表中信息可以判断该足球训练队队员年龄的众数为( )
A.14
B.15
C.16
D.17
查看答案和解析>>
科目:初中数学 来源: 题型:
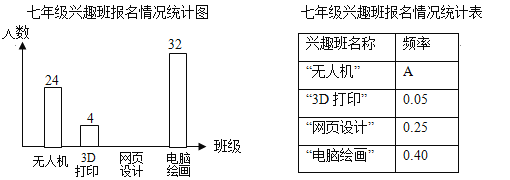
【题目】学校计划在七年级学生中开设4个信息技术应用兴趣班,分别为“无人机”班,“3D打印”班,“网页设计”班,“电脑绘画”班,规定每人最多参加一个班,自愿报名.根据报名情况绘制了下面统计图表,请回答下列问题:
(1)报名参加兴趣班的总人数为 人;统计表中的A= ;
(2)将统计图补充完整;
(3)为了均衡班级人数,在“电脑绘画”班中至少动员几人到“3D打印”班,才能使“电脑绘画”班人数不超过“3D打印”班人数的2倍?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个大小不同的等腰直角三角形三角板如图①所示放置,图②是由它抽象出的几何图形,B,C,E在同一条直线上,连接DC, 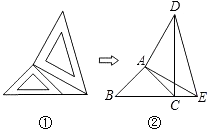
(1)请找出图②中的全等三角形,并给予说明(说明:结论中不得含有未标识的字母);
(2)试说明:DC⊥BE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com