
【题目】如图,在等边三角形ABC中,点E、D分别从A、C出发,沿AC,CB方向以相同的速度在线段AC,CB上运动,AD、BE相交于F点. 
(1)求证:△ABE≌△CAD;
(2)当E、D运动时,∠BFD大小是否发生改变?若不变求其大小,若改变求其变化范围.
【答案】
(1)解:∵△ABC是等边三角形,
∴AC=AB,∠C=∠BAE=60°,
∵点E、D分别从A、C出发,沿AC,CB方向以相同的速度在线段AC,CB上运动,
∴BD=CE,
∴AE=CD,
在△ABE和△CAD中,
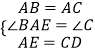 ,
,
∴△ABE≌△CAD
(2)解:当E、D运动时,∠BFD大小不发生改变,
∵△ABE≌△CAD,
∴∠ABE=∠CAD,
∵∠AFE=∠ABE+∠BAF,
∴∠AFE=∠CAD+∠BAF=∠BAC=60°,
∵∠AFE=∠BFD(对顶角相等),
∴∠BFD=60°
【解析】(1)由等边三角形ABC可得出的条件是:AB=AC,∠BAC=∠ACB=60°,可根据SAS证明△ABE≌△CAD;(2)E、D运动时,∠BFD大小不发生改变,根据△ABE≌△CAD,得到∠ABE=∠CAD,利用外角的性质得到∠AFE=∠ABE+∠BAF,再根据对顶角相等,即可解答.
【考点精析】根据题目的已知条件,利用等边三角形的性质的相关知识可以得到问题的答案,需要掌握等边三角形的三个角都相等并且每个角都是60°.


科目:初中数学 来源: 题型:
【题目】两个大小不同的等腰直角三角形三角板如图①所示放置,图②是由它抽象出的几何图形,B,C,E在同一条直线上,连接DC, 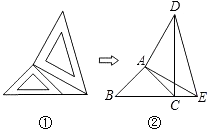
(1)请找出图②中的全等三角形,并给予说明(说明:结论中不得含有未标识的字母);
(2)试说明:DC⊥BE.
查看答案和解析>>
科目:初中数学 来源: 题型:
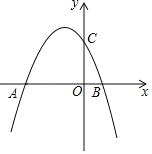
【题目】如图,已知抛物线y=-![]() x2+bx+6与x轴交于点A(﹣6,0)和点B,与y轴交于点C.
x2+bx+6与x轴交于点A(﹣6,0)和点B,与y轴交于点C.
(1)求该抛物线的解析式;
(2)写出顶点的坐标,并求AB的长;
(3)若点A,O,C均在⊙D上,请写出点D的坐标,连接BC,并判断直线BC与⊙D的位置关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,AB=AC,以AC边为直径作⊙O交BC边于点D,过点D作
中,AB=AC,以AC边为直径作⊙O交BC边于点D,过点D作![]() 于点E,ED、AC的延长线交于点F.
于点E,ED、AC的延长线交于点F.
(1)求证:EF是⊙O的切线;
(2)若![]() 且
且![]() ,求⊙O的半径与线段AE的长.
,求⊙O的半径与线段AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国正在建设的港珠澳大桥,是连接香港、珠海、澳门的超大型跨海大桥隧道,建成后将成为世界最大的跨海大桥,全长55000米,用科学记数法表示55000为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ACB中,∠ACB=90°,∠ABC=30°,AC=1,点D为AC上一动点,连接BD,以BD为边作等边△BDE,设CD=n. 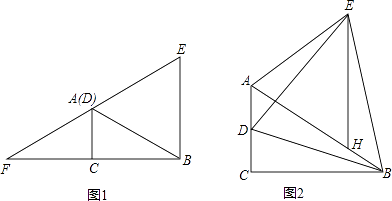
(1)当n=1时,EA的延长线交BC的延长线于F,则AF=;
(2)当0<n<1时,如图2,在BA上截取BH=AD,连接EH.
①设∠CBD=x,用含x的式子表示∠ADE和∠ABE.
②求证:△AEH为等边三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
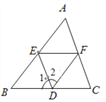
【题目】如图,(1)如果∠1=__________,那么DE∥AC;(同位角相等,两直线平行);
(2)如果∠1=__________,那么EF∥BC;(内错角相等,两直线平行);
(3)如果∠DEF+__________=180°,那么DE∥AC;(同旁内角互补,两直线平行);
(4)如果∠2+__________=180°,那么AB∥DF;(同旁内角互补,两直线平行).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com