
【题目】已知抛物线与x轴交于A(-1,0)和B(3,0)两点,且与y轴交于点C(0,3).
(1)求抛物线的解析式;
(2)抛物线的对称轴方程和顶点M坐标;
(3)求四边形ABMC的面积.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)9
;(3)9
【解析】
(1)已知了三点的坐标,可用交点式二次函数通式来设抛物线的解析式然后将C点的坐标代入抛物线中即可求出抛物线的解析式;
(2)根据(1)得出的抛物线的解析式即可求出对称轴方程及M的坐标(可用配方法进行求解);
(3)由于四边形ABMC不是规则的四边形,因此可过M作x轴的垂线,将四边形ABMC分成梯形和两个直角三角形三部分来求.
解:(1)由题意,可设抛物线的解析式为y=a(x+1)(x3),
将C点坐标代入后可得:3=a(0+1)(03),
解得a=1,
∴抛物线的解析式为:y=(x+1)(x3)=x2+2x+3;
(2)由(1)的抛物线的解析式可知:y=x2+2x+3=(x1)2+4,
∴抛物线的对称轴方程为:x=1,顶点M的坐标为:M(1,4);
(3)过M作MN⊥x轴于N,
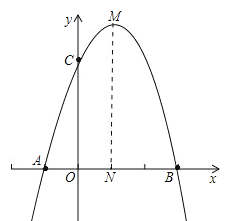
则有S四边形ABMC=S△AOC+S△BMN+S梯形MNOC
=![]() OAOC+
OAOC+![]() BNMN+
BNMN+![]() (OC+MN)ON
(OC+MN)ON
=![]() ×1×3+
×1×3+![]() ×2×4+
×2×4+![]() ×(3+4)×1
×(3+4)×1
=9,
∴四边形ABMC的面积为9.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图所示,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(1,0)和点B,与y轴的正半轴交于点C.现有下列结论:①abc>0;②4a﹣2b+c>0;③2a﹣b>0;④3a+c=0,其中,正确结论的个数是( )
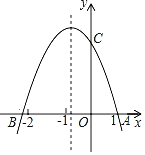
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形![]() 内接于
内接于![]() ,点
,点![]() 为
为![]() 上一点,连接
上一点,连接![]() 、
、![]() 、
、![]() .
.
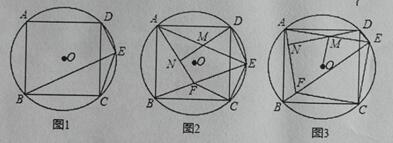
(1)如图1,求证:∠DEC+∠BEC= 180°;
(2)如图2,过点C作CF⊥CE交BE于点F,连接AF, M为AE的中点,连接DM并延长交AF于点N,求证: DN⊥AF;
(3)如图3,在(2) 的条件下,连接OM,若AB=10,![]() 求OM的长.
求OM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现
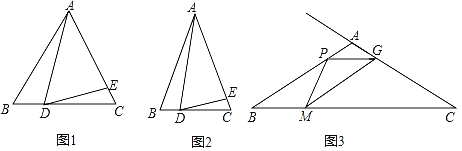
如图1,![]() ABC是等边三角形,点D,E分别在边BC,AC上,若∠ADE=60°,则AB,CE,BD,DC之间的数量关系是 .
ABC是等边三角形,点D,E分别在边BC,AC上,若∠ADE=60°,则AB,CE,BD,DC之间的数量关系是 .
(2)拓展探究
如图2,![]() ABC是等腰三角形,AB=AC,∠B=α,点D,E分别在边BC,AC上.若∠ADE=α,则(1)中的结论是否仍然成立?请说明理由.
ABC是等腰三角形,AB=AC,∠B=α,点D,E分别在边BC,AC上.若∠ADE=α,则(1)中的结论是否仍然成立?请说明理由.
(3)解决问题
如图3,在![]() ABC中,∠B=30°,AB=AC=4cm,点P从点A出发,以1cm/s的速度沿A→B方向勾速运动,同时点M从点B出发,以
ABC中,∠B=30°,AB=AC=4cm,点P从点A出发,以1cm/s的速度沿A→B方向勾速运动,同时点M从点B出发,以![]() cm/s的速度沿B→C方向匀速运动,当其中一个点运动至终点时,另一个点随之停止运动,连接PM,在PM右侧作∠PMG=30°,该角的另一边交射线CA于点G,连接PC.设运动时间为t(s),当△APG为等腰三角形时,直接写出t的值.
cm/s的速度沿B→C方向匀速运动,当其中一个点运动至终点时,另一个点随之停止运动,连接PM,在PM右侧作∠PMG=30°,该角的另一边交射线CA于点G,连接PC.设运动时间为t(s),当△APG为等腰三角形时,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】伊利集团是中国规模最大、产品线最全的乳制品企业.综合实践小组的同学从网上搜集到如下一些伊利集团近几年的营业状况的资料,其中图1是2013-2018年伊利集团营业收入及净利润情况统计图,图2是2018年伊利集团各品类业务营业、收入比例情况统计图(数据来源:公司财报、中商产业研究院).
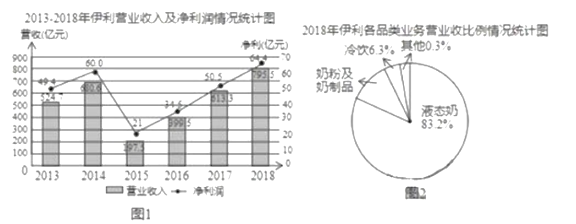
综合实践小组的同学结合统计图提出了如下问题,请你解答:
(1)2018年,伊利集团营收及净利再次刷新行业记录,稳居亚洲乳业第一,这一年,伊利集团实现营业收入 亿元,净利润 亿元.
(2)求2018年伊利集团“奶粉及奶制品”业务的营业收入(结果精确到![]() 亿元).
亿元).
(3)在2013-2018这![]() 年中,伊利集团的净利比上一年增长额最多的是 年;估计2019年伊利集团的净利润将比上一年增长 亿元,并说明理由.
年中,伊利集团的净利比上一年增长额最多的是 年;估计2019年伊利集团的净利润将比上一年增长 亿元,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() 点
点![]() 是直线
是直线![]() 上的一动点(不与点
上的一动点(不与点![]() 重合),连接
重合),连接![]() 在
在![]() 的右侧以
的右侧以![]() 为斜边作等腰直角三角形
为斜边作等腰直角三角形![]() .点
.点![]() 是
是![]() 的中点,连接
的中点,连接![]() .
.
[问题发现]
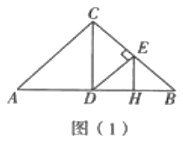
(1)如图(1),当点![]() 是
是![]() 的中点时,线段
的中点时,线段![]() 与
与![]() 的数量关系是______,
的数量关系是______,![]() 与
与![]() 的位置关系是______;
的位置关系是______;
[猜想论证]
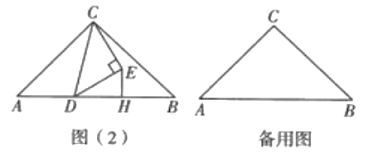
(2)如图(2),当点![]() 在边
在边![]() 上且不是
上且不是![]() 的中点时,(1)中的结论是否仍然成立?若成立,请仅就图(2)中的情况给出证明;若不成立,请说明理由.
的中点时,(1)中的结论是否仍然成立?若成立,请仅就图(2)中的情况给出证明;若不成立,请说明理由.
[拓展应用]
(3)若![]() ,其他条件不变,连接
,其他条件不变,连接![]() .当
.当![]() 是等边三角形时,请直接写出
是等边三角形时,请直接写出![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明大学毕业回家乡创业,第一期培植盆景与花卉各50盆售后统计,盆景的平均每盆利润是160元,花卉的平均每盆利润是19元,调研发现:
①盆景每增加1盆,盆景的平均每盆利润减少2元;每减少1盆,盆景的平均每盆利润增加2元;②花卉的平均每盆利润始终不变.
小明计划第二期培植盆景与花卉共100盆,设培植的盆景比第一期增加x盆,第二期盆景与花卉售完后的利润分别为W1,W2(单位:元)
(1)用含x的代数式分别表示W1,W2;
(2)当x取何值时,第二期培植的盆景与花卉售完后获得的总利润W最大,最大总利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com