
【题目】已知正方形![]() 内接于
内接于![]() ,点
,点![]() 为
为![]() 上一点,连接
上一点,连接![]() 、
、![]() 、
、![]() .
.
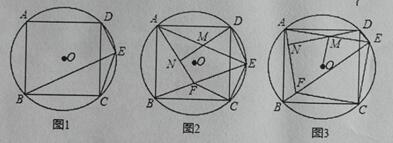
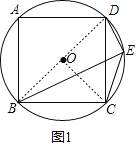
(1)如图1,求证:∠DEC+∠BEC= 180°;
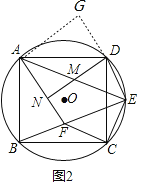
(2)如图2,过点C作CF⊥CE交BE于点F,连接AF, M为AE的中点,连接DM并延长交AF于点N,求证: DN⊥AF;
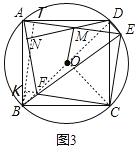
(3)如图3,在(2) 的条件下,连接OM,若AB=10,![]() 求OM的长.
求OM的长.
【答案】(1)证明过程见解析;(2)证明过程见解析;(3)![]() ;
;
【解析】
(1)连接BD,OC,得出∠BEC=45°,由圆周角定理可得出结论
(2)延长ED至G,使ED=DG,连接AG,证明△BFC≌△DEC,可得出BF=DE,证明△ABF≌△ADG,则∠BAF=∠DAC,证明DM∥AG,得出∠DNF=∠FAG=90°,则可得出结论;
(3)连接BD,OC,过点B作BK⊥CF交CF的延长线于点K,过点B作BT⊥AE于点T,设DE=x,则BE=7x,得出BD=5![]() x,求出x=2,求出BK=KF=
x,求出x=2,求出BK=KF=![]() ,由tan∠BCF=tan∠DCE=
,由tan∠BCF=tan∠DCE=![]() ,求出CF,可求出TB=7
,求出CF,可求出TB=7![]() ,AM=4
,AM=4![]() ,则可求出OM的长.
,则可求出OM的长.
解:(1)证明:连接BD,OC,
∵四边形ABCD为正方形,
∴∠A=90°,BC= CD,
∴BD为⊙O的直径,即∠DEB=90°,
∵OB= OD,
∴OC⊥BD,即∠BOC= 90°,
∴∠BEC=![]() ∠ BOC=45°,
∠ BOC=45°,
∴∠DEC+∠BEC=∠DEB+∠BEC+∠BEC= 180°.
(2)证明:如图,延长ED至G,使ED=DG,连接AG,
∵CE⊥CF,∴∠ECF=90°,
∵∠CEF=45°,
∴∠CEF=∠CFE=45°,
∴CE= CF,
∵∠BCD=∠ECF=90°,
∴∠BCF=∠DCE,
∵BC=CD,
∴△BFC≌ODEC (SAS),即BF=DE ,
∵DE=DG,
∴BF=DG,
∵四边形ABED为圆O的内接四边形,
∴∠ABE+∠ADE= 180°,
∴∠ADE+∠ADG=180°,
∴∠ABE=∠ADG,
∵AB=AD,
∴△ABF≌OADG (SAS), 即∠BAF=∠DAG,
∵∠BAF+∠FAD=∠BAD=90°,
∴∠DAG+∠FAD=90°,即∠FAG= 90°.
∵M为AE的中点,
∴DM为△AEG的中位线,即DM// AG,
∴∠DNF=∠FAG=90°,即DN⊥AF.
(3)解:如图,连接BD,OC,过B作BK⊥CF的延长线于点K,
过点B作BT⊥AE于T,
由(1)知![]() ,则
,则![]() ,
,
由(1)知BD为⊙O的直径,
在![]() 中,
中,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
设DE=x,则BE=7x,
在![]() 中,
中,![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,即
,即![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
由(2)知![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,即
,即![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∵![]() 为
为![]() 的中点,∴
的中点,∴![]() ,
,
在![]() 中,
中,![]() .
.


科目:初中数学 来源: 题型:
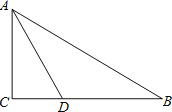
【题目】已知:如图,在![]() 中,
中,![]() 的角平分线
的角平分线![]() 交
交![]() 边于
边于![]() .
.
(1)以![]() 边上一点
边上一点![]() 为圆心,过
为圆心,过![]() 两点作
两点作![]() (不写作法,保留作图痕迹),再判断直线
(不写作法,保留作图痕迹),再判断直线![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)若(1)中的![]() 与
与![]() 边的另一个交点为
边的另一个交点为![]() ,
,![]() ,求线段
,求线段![]() 与劣弧
与劣弧![]() 所围成的图形面积.(结果保留根号和
所围成的图形面积.(结果保留根号和![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某报社为了解市民对“社会主义核心价值观”的知晓程度,采取随机抽样的方式进行问卷调查,调查结果分为“A.非常了解”、“B.了解”、“C.基本了解”三个等级,并根据调查结果绘制了如下两幅不完整的统计图.
(1)这次调查的市民人数为________人,m=________,n=________;
(2)补全条形统计图;
(3)若该市约有市民100000人,请你根据抽样调查的结果,估计该市大约有多少人对“社会主义核心价值观”达到“A.非常了解”的程度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在每个小正方形的边长为1的网格中,![]() 的顶点A,B,O均落在格点上,
的顶点A,B,O均落在格点上,![]() 为⊙O的半径.
为⊙O的半径.
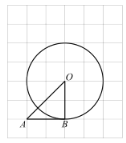
(1)![]() 的大小等于_________(度);
的大小等于_________(度);
(2)将![]() 绕点O顺时针旋转,得
绕点O顺时针旋转,得![]() ,点A,B旋转后的对应点为
,点A,B旋转后的对应点为![]() ,
,![]() .连接
.连接![]() ,设线段
,设线段![]() 的中点为M,连接
的中点为M,连接![]() .当
.当![]() 取得最大值时,请在如图所示的网格中,用无刻度的直尺画出点
取得最大值时,请在如图所示的网格中,用无刻度的直尺画出点![]() ,并简要说明点
,并简要说明点![]() 的位置是如何找到的(不要求证明).
的位置是如何找到的(不要求证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
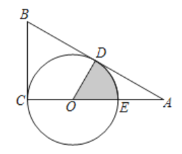
【题目】如图,O为Rt△ABC直角边AC上一点,以OC为半径作⊙O与斜边AB相切于点D,交OA于点E,已知![]() ,AC=3,则图中阴影部分的面积是__________.
,AC=3,则图中阴影部分的面积是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
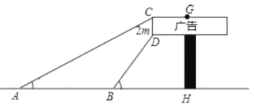
【题目】数学小组想利用所学的知识了解某广告牌的高度(图中![]() 的长),经测量知
的长),经测量知![]() ,在B处测得点D的仰角为
,在B处测得点D的仰角为![]() ,在A处测得点C的仰角为
,在A处测得点C的仰角为![]() ,
,![]() ,且A、B、H三点在一条直线上,请根据以上数据计算GH的长(
,且A、B、H三点在一条直线上,请根据以上数据计算GH的长(![]() ,要求结果精确得到0.1
,要求结果精确得到0.1![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小雨、小华、小星暑假到某超市参加社会实践活动,在活动中他们参加了某种水果的销售工作,已知该水果的进价为8元/千克.他们通过市场调查发现:当销售单价为10元时,那么每天可售出300千克;销售单价每上涨1元,每天的销售量就减少50千克.
(1)求该超市销售这种水果,每天的销售量y(千克)与销售单价x(元/千克)之间的函数关系式;
(2)一段时间后,发现这种水果每天的销售量均不低于250千克,则此时该超市销售这种水果每天获取的利润w(元)最大是多少?
(3)为响应政府号召,该超市决定在暑假期间每销售1千克这种水果就捐赠a元利润(a≤2.5)给希望工程.公司通过销售记录发现,当销售单价不超过13元时,每天扣除捐赠后的日销售利润随销售单价x(元/千克)的增大而增大,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线与x轴交于A(-1,0)和B(3,0)两点,且与y轴交于点C(0,3).
(1)求抛物线的解析式;
(2)抛物线的对称轴方程和顶点M坐标;
(3)求四边形ABMC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解市民对“垃圾分类知识”的知晓程度,某数学学习兴趣小组对市民进行 随机抽样的问卷调查,调查结果分为“A.非常了解”、“B.了解”、“C.基本了解”、“D.不太了解”四个等级进行统计,并将统计结果绘制成如下两幅不完整的统计图(图1,图2), 请根据图中的信息解答下列问题.
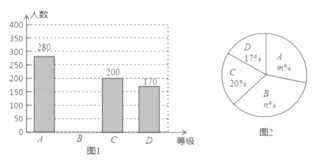
(1)这次调查的市民人数为________人,图2中,![]() _________;
_________;
(2)图1中的条形统计图中B等级的人数;
(3)在图2中的扇形统计图中,求“C.基本了解”所在扇形的圆心角度数;
(4)据统计,2018年该市约有市民500万人,那么根据抽样调查的结果,可估计对“垃圾分类知识”的知晓程度为“A.非常了解”的市民约有多少万人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com