
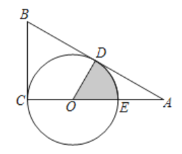
【题目】如图,O为Rt△ABC直角边AC上一点,以OC为半径作⊙O与斜边AB相切于点D,交OA于点E,已知![]() ,AC=3,则图中阴影部分的面积是__________.
,AC=3,则图中阴影部分的面积是__________.
【答案】![]()
【解析】
首先利用勾股定理求出AB的长,再证明BD=BC,进而由AD=AB-BD可求出AD的长度;利用特殊角的锐角三角函数可求出∠A的度数,则圆心角∠DOA的度数可求出,在直角三角形ODA中求出OD的长,最后利用扇形的面积公式即可求出阴影部分的面积.
解:在Rt△ABC中,∵BC=![]() ,AC=3.
,AC=3.
∴AB=![]() =2
=2![]() ,
,
∵BC⊥OC,
∴BC是圆的切线,
∵⊙O与斜边AB相切于点D,
∴BD=BC=![]() ,
,
∴AD=AB-BD=2![]() -
-![]() =
=![]() ;
;
在Rt△ABC中,∵sinA=![]() =
=![]() =
=![]() ,
,
∴∠A=30°,
∵⊙O与斜边AB相切于点D,
∴OD⊥AB,
∴∠AOD=90°-∠A=60°,
∵![]() =tanA=tan30°,
=tanA=tan30°,
∴![]() =
=![]() .
.
∴OD=1,
∴S阴影=![]() =
=![]() .
.
故答案是:![]()


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:
【题目】2022年在北京将举办第24届冬季奥运会,很多学校都开展了冰雪项目学习.如图,滑雪轨道由AB、BC两部分组成,AB、BC的长度都为200米,一位同学乘滑雪板沿此轨道由A点滑到了C点,若AB与水平面的夹角α为20°,BC与水平面的夹角β为45°,则他下降的高度为___________米(精确到1米,![]() ,sin20o=0.3420,tan20o=0.3640,cos20o=0.9400).
,sin20o=0.3420,tan20o=0.3640,cos20o=0.9400).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作DE⊥AB,垂足为E.

(1)求证:DE是⊙O的切线;
(2)若DE= ![]() ,∠C=30°,求
,∠C=30°,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 与一次函数
与一次函数![]() 的图象交于点
的图象交于点![]() 与反比例函数
与反比例函数![]() 的图象交于点
的图象交于点![]() ,点
,点![]() 与点
与点![]() 关于
关于![]() 轴对称.
轴对称.
(1)直接写出点![]() 的坐标;
的坐标;
(2)求点![]() 的坐标(用含
的坐标(用含![]() 的式子表示);
的式子表示);
(3)若![]() 两点中只有一个点在线段
两点中只有一个点在线段![]() 上,直接写出
上,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂生产某种产品,每件产品的出厂价为50元,成本为25元.由于在生产过程中,平均每生产1件产品,有![]() 污水排出,所以为了净化环境,工厂设计两种方案对污水进行处理,并准备实施.
污水排出,所以为了净化环境,工厂设计两种方案对污水进行处理,并准备实施.
方案甲:工厂将污水排到污水厂统一处理,每处理![]() 需付14元的排污费;
需付14元的排污费;
方案乙:工厂将污水进行净化处理后再排出,每处理![]() 污水所用原料费为2元,且每月净化设备的损耗费为30000元.设工厂每月生产x件产品(x为正整数,
污水所用原料费为2元,且每月净化设备的损耗费为30000元.设工厂每月生产x件产品(x为正整数,![]() ).
).
(1)根据题意填写下表:
每月生产产品的数量/件 | 3500 | 4500 | 5500 | … |
方案甲处理污水的费用/元 | 31500 | … | ||
方案乙处理污水的费用/元 | 34500 | … |
(2)设工厂按方案甲处理污水时每月获得的利润为![]() 元,按方案乙处理污水时每月获得的利润为
元,按方案乙处理污水时每月获得的利润为![]() 元,分别求
元,分别求![]() ,
,![]() 关于x的函数解析式;
关于x的函数解析式;
(3)根据题意填空:
①若该工厂按方案甲处理污水时每月获得的利润和按方案乙处理污水时每月获得利润相同,则该工厂每月生产产品的数量为_______件;
②若该工厂每月生产产品的数量为7500件时,则该工厂选用方案甲、方案乙中的方案_______处理污水时所获得的利润多;
③若该工厂每月获得的利润为81000元,则该工厂选用方案甲、方案乙中的方案________处理污水时生产产品的数量少.
查看答案和解析>>
科目:初中数学 来源: 题型:
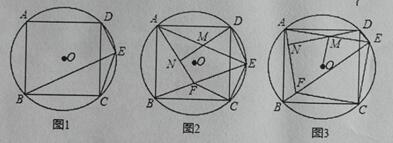
【题目】已知正方形![]() 内接于
内接于![]() ,点
,点![]() 为
为![]() 上一点,连接
上一点,连接![]() 、
、![]() 、
、![]() .
.
(1)如图1,求证:∠DEC+∠BEC= 180°;
(2)如图2,过点C作CF⊥CE交BE于点F,连接AF, M为AE的中点,连接DM并延长交AF于点N,求证: DN⊥AF;
(3)如图3,在(2) 的条件下,连接OM,若AB=10,![]() 求OM的长.
求OM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是半圆
是半圆![]() 的直径,
的直径,![]() .射线
.射线![]() 为半圆
为半圆![]() 的切线.在
的切线.在![]() 上取一点
上取一点![]() ,连接
,连接![]() 交半圆于点
交半圆于点![]() ,连接
,连接![]() .过
.过![]() 点作
点作![]() 的垂线
的垂线![]() ,垂足为点
,垂足为点![]() ,与
,与![]() 相交于点
相交于点![]() .过
.过![]() 点作半圆
点作半圆![]() 的切线
的切线![]() ,切点为
,切点为![]() ,与
,与![]() 相交于点
相交于点![]() .
.

(1)求证:![]() ∽
∽![]() ;
;
(2)当![]() 与
与![]() 的面积相等时,求
的面积相等时,求![]() 的长;
的长;
(3)求证:当![]() 在
在![]() 上移动时(
上移动时(![]() 点除外),点
点除外),点![]() 始终是线段
始终是线段![]() 的中点.
的中点.
查看答案和解析>>
科目:初中数学 来源: 题型:
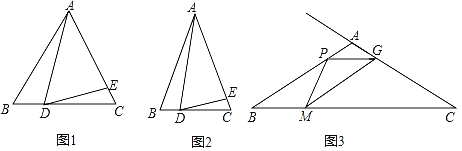
【题目】(1)问题发现
如图1,![]() ABC是等边三角形,点D,E分别在边BC,AC上,若∠ADE=60°,则AB,CE,BD,DC之间的数量关系是 .
ABC是等边三角形,点D,E分别在边BC,AC上,若∠ADE=60°,则AB,CE,BD,DC之间的数量关系是 .
(2)拓展探究
如图2,![]() ABC是等腰三角形,AB=AC,∠B=α,点D,E分别在边BC,AC上.若∠ADE=α,则(1)中的结论是否仍然成立?请说明理由.
ABC是等腰三角形,AB=AC,∠B=α,点D,E分别在边BC,AC上.若∠ADE=α,则(1)中的结论是否仍然成立?请说明理由.
(3)解决问题
如图3,在![]() ABC中,∠B=30°,AB=AC=4cm,点P从点A出发,以1cm/s的速度沿A→B方向勾速运动,同时点M从点B出发,以
ABC中,∠B=30°,AB=AC=4cm,点P从点A出发,以1cm/s的速度沿A→B方向勾速运动,同时点M从点B出发,以![]() cm/s的速度沿B→C方向匀速运动,当其中一个点运动至终点时,另一个点随之停止运动,连接PM,在PM右侧作∠PMG=30°,该角的另一边交射线CA于点G,连接PC.设运动时间为t(s),当△APG为等腰三角形时,直接写出t的值.
cm/s的速度沿B→C方向匀速运动,当其中一个点运动至终点时,另一个点随之停止运动,连接PM,在PM右侧作∠PMG=30°,该角的另一边交射线CA于点G,连接PC.设运动时间为t(s),当△APG为等腰三角形时,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
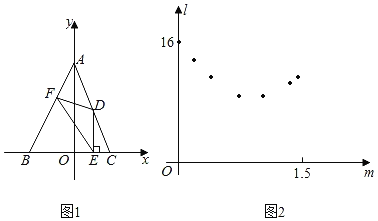
【题目】如图1,在平面直角坐标系中,△ABC的顶点A,C分別是直线y=﹣![]() x+4与坐标轴的交点,点B的坐标为(﹣2,0),点D是边AC上的一点,DE⊥BC于点E,点F在边AB上,且D,F两点关于y轴上的某点成中心对称,连结DF,EF.设点D的横坐标为m,EF2为l,请探究:
x+4与坐标轴的交点,点B的坐标为(﹣2,0),点D是边AC上的一点,DE⊥BC于点E,点F在边AB上,且D,F两点关于y轴上的某点成中心对称,连结DF,EF.设点D的横坐标为m,EF2为l,请探究:
①线段EF长度是否有最小值.
②△BEF能否成为直角三角形.
小明尝试用“观察﹣猜想﹣验证﹣应用”的方法进行探究,请你一起来解决问题.
(1)小明利用“几何画板”软件进行观察,测量,得到l随m变化的一组对应值,并在平面直角坐标系中以各对应值为坐标描点(如图2).请你在图2中连线,观察图象特征并猜想l与m可能满足的函数类别.
(2)小明结合图1,发现应用三角形和函数知识能验证(1)中的猜想,请你求出l关于m的函数表达式及自变量的取值范围,并求出线段EF长度的最小值.
(3)小明通过观察,推理,发现△BEF能成为直角三角形,请你求出当△BEF为直角三角形时m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com