
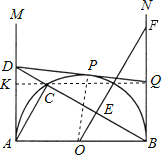
【题目】如图,![]() 是半圆
是半圆![]() 的直径,
的直径,![]() .射线
.射线![]() 为半圆
为半圆![]() 的切线.在
的切线.在![]() 上取一点
上取一点![]() ,连接
,连接![]() 交半圆于点
交半圆于点![]() ,连接
,连接![]() .过
.过![]() 点作
点作![]() 的垂线
的垂线![]() ,垂足为点
,垂足为点![]() ,与
,与![]() 相交于点
相交于点![]() .过
.过![]() 点作半圆
点作半圆![]() 的切线
的切线![]() ,切点为
,切点为![]() ,与
,与![]() 相交于点
相交于点![]() .
.

(1)求证:![]() ∽
∽![]() ;
;
(2)当![]() 与
与![]() 的面积相等时,求
的面积相等时,求![]() 的长;
的长;
(3)求证:当![]() 在
在![]() 上移动时(
上移动时(![]() 点除外),点
点除外),点![]() 始终是线段
始终是线段![]() 的中点.
的中点.
【答案】(1)证明见解析;(2)BQ=1;(3)证明见解析.
【解析】
(1)根据OE∥AC,得出∠BAC=∠FOB,进而得出∠BCA=∠FBO=90°,从而证明结论;
(2)根据△ACB∽△OBF得出△ABD∽△BFO,从而得出DQ∥AB,即可得出BQ=AD;
(3)首先得出AD=DP,QB=BQ,进而得出DQ2=QK2+DK2,得出BF=2BQ,即可得出Q为BF的中点.
解:(1)证明:∵AB为直径,
∴∠ACB=90°,即:AC⊥BC,
又OE⊥BC,
∴OE∥AC,
∴∠BAC=∠FOB,
∵BN是半圆的切线,
∴∠BCA=∠FBO=90°,
∴△ABC∽△OFB.
(2)连接OP,
由△ACB∽△OBF得,∠OFB=∠DBA,∠BCA=∠FBO=90°,
∵AM、BN是⊙O的切线,
∴∠DAB=∠OBF=90°,
∴△ABD∽△BFO,
∴当△ABD与△BFO的面积相等时,△ABD≌△BFO,
∴AD=OB=1,
∵DP切圆O,DA切圆O,
∴DP=DA,
∵△ABD≌△BFO,
∴DA=BO=PO=DP,
又∵∠DAO=∠DPO=90°,
∴四边形AOPD是正方形,
∴DQ∥AB,
∴四边形ABQD是矩形,
∴BQ=AD=1;
(3)证明:由(2)知,△ABD∽△BFO,
∴![]() =
=![]() ,
,
∴BF=![]() =
=![]() =
=![]() ,
,
∵DP是半圆O的切线,射线AM、BN为半圆O的切线,
∴AD=DP,QB=QP,
过Q点作AM的垂线QK,垂足为K,在Rt△DQK中,
DQ2=QK2+DK2,
∴(AD+BQ)2=(AD﹣BQ)2+22.
∴BQ=![]() ,
,
∴BF=2BQ,
∴Q为BF的中点.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】![]() 两地相距
两地相距![]() ,甲、乙两人从两地出发相向而行,甲先出发.图中
,甲、乙两人从两地出发相向而行,甲先出发.图中![]() 表示两人离
表示两人离![]() 地的距离
地的距离![]() 与时间
与时间![]() 的关系,结合图象,下列结论错误的是( )
的关系,结合图象,下列结论错误的是( )
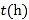
A.![]() 是表示甲离
是表示甲离![]() 地的距离与时间关系的图象
地的距离与时间关系的图象
B.乙的速度是![]()
C.两人相遇时间在![]()
D.当甲到达终点时乙距离终点还有![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据规定,我市将垃圾分为了四类:可回收物、易腐垃圾、有害垃圾和其他垃圾四大类.现有投放这四类垃圾的垃圾桶各1个,若将用不透明垃圾袋分类打包好的两袋不同垃圾随机投进两个不同的垃圾桶,投放正确的概率是______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
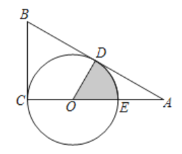
【题目】如图,O为Rt△ABC直角边AC上一点,以OC为半径作⊙O与斜边AB相切于点D,交OA于点E,已知![]() ,AC=3,则图中阴影部分的面积是__________.
,AC=3,则图中阴影部分的面积是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
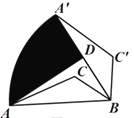
【题目】如图,在△ABC中,AB=4,若将△ABC绕点B顺时针旋转60°,点A的对应点为点A′,点C的对应点为点C′,点D为A′B的中点,连接AD.则点A的运动路径![]() 与线段AD、A′D围成的阴影部分面积是______.
与线段AD、A′D围成的阴影部分面积是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小雨、小华、小星暑假到某超市参加社会实践活动,在活动中他们参加了某种水果的销售工作,已知该水果的进价为8元/千克.他们通过市场调查发现:当销售单价为10元时,那么每天可售出300千克;销售单价每上涨1元,每天的销售量就减少50千克.
(1)求该超市销售这种水果,每天的销售量y(千克)与销售单价x(元/千克)之间的函数关系式;
(2)一段时间后,发现这种水果每天的销售量均不低于250千克,则此时该超市销售这种水果每天获取的利润w(元)最大是多少?
(3)为响应政府号召,该超市决定在暑假期间每销售1千克这种水果就捐赠a元利润(a≤2.5)给希望工程.公司通过销售记录发现,当销售单价不超过13元时,每天扣除捐赠后的日销售利润随销售单价x(元/千克)的增大而增大,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
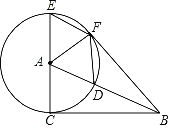
【题目】如图,在![]() ABC中,∠ACB=90°,以点A为圆心,AC的长为半径作⊙A,交AB于点D,交CA的延长线于点E.过点E作EF∥AB,交⊙A于点F,连接AF,BF,DF.
ABC中,∠ACB=90°,以点A为圆心,AC的长为半径作⊙A,交AB于点D,交CA的延长线于点E.过点E作EF∥AB,交⊙A于点F,连接AF,BF,DF.
(1)求证:BF是⊙A的切线;
(2)填空:
①当四边形ADFE是周长为20的菱形时,BF= ;
②当![]() = 时,四边形ACBF是正方形.
= 时,四边形ACBF是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据市卫生防疫部门的要求,游泳池必须定期换水后才能对外开放.在换水时需要经“排水一清冼一灌水”的过程.某游泳馆从早上![]() 开始对游泳池进行换水,已知该游泳池的排水速度是灌水速度的
开始对游泳池进行换水,已知该游泳池的排水速度是灌水速度的![]() 倍,其中游泳池内剩余的水量
倍,其中游泳池内剩余的水量![]() 与换水时间上
与换水时间上![]() 之间的函数图象如图所示,根据图象解答下列问题:
之间的函数图象如图所示,根据图象解答下列问题:
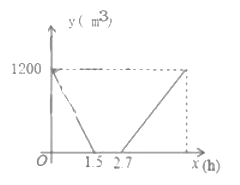
(1)该游泳池清洗需要 小时.
(2)求排水过程中的![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围.
的取值范围.
(3)若该游泳馆在换水结束![]() 分钟后才能对外开放,判断游泳爱好者小致能否在中午
分钟后才能对外开放,判断游泳爱好者小致能否在中午![]() 进入该游泳馆游泳,并说明理由.
进入该游泳馆游泳,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们把有一组邻边相等,一组对边平行但不相等的四边形称作“准菱形”.
(1)证明“准菱形”性质:“准菱形”的一条对角线平分一个内角.
(要求:根据图1写出已知,求证,证明)
已知:
求证:
证明:
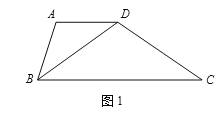
(2)已知.在△ABC中,∠A=90°,AB=3,AC=4.若点D,E分别在边BC,AC上,且四边形ABDE为“准菱形”.请在下列给出的△ABC中,作出满足条件的所有“准菱形”ABDE,并写出相应DE的长.(所给△ABC不一定都用,不够可添)
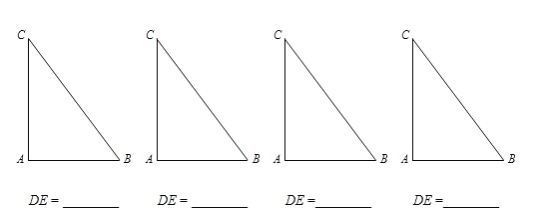
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com