练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】根据规定，我市将垃圾分为了四类：可回收物、易腐垃圾、有害垃圾和其他垃圾四大类．现有投放这四类垃圾的垃圾桶各1个，若将用不透明垃圾袋分类打包好的两袋不同垃圾随机投进两个不同的垃圾桶，投放正确的概率是______________．

    【答案】

    【解析】

    根据题意画出树状图，再根据概率公式即可求解．

    解：可回收物、易腐垃圾、有害垃圾和其他垃圾四大类对应的垃圾筒分别用A，B，C，D表示，垃圾分别用a，b，c，d表示．设分类打包好的两袋不同垃圾为a、b，

    画树状图如图：

    共有12个等可能的结果，分类打包好的两袋不同垃圾随机投入进两个不同的垃圾桶，投放正确的结果有1个，

    ∴分类打包好的两袋不同垃圾随机投入进两个不同的垃圾桶，投放正确的概率为，

    故答案为：．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC中，∠BCA=90°，CD是边AB上的中线，分别过点C，D作BA和BC的平行线，两线交于点E，且DE交AC于点O，连接AE．

    （1）求证：四边形ADCE是菱形；

    （2）若∠B=60°，BC=6，求四边形ADCE的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，的半径为6，是的内接三角形，连接、，若与互补，则线段的长为______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在等腰△ABC中，AB=AC，以AC为直径作⊙O交BC于点D，过点D作DE⊥AB，垂足为E．

    （1）求证：DE是⊙O的切线；

    （2）若DE= ，∠C=30°，求的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】 我们定义：如图1、图2、图3，在△ABC中，把AB绕点A顺时针旋转α（0°＜α＜180°）得到AB′，把AC绕点A逆时针旋转β得到AC′，连接B′C′，当α+β＝180°时，我们称△AB'C′是△ABC的“旋补三角形”，△AB′C′边B'C′上的中线AD叫做△ABC的“旋补中线”，点A叫做“旋补中心”．图1、图2、图3中的△AB′C′均是△ABC的“旋补三角形”．

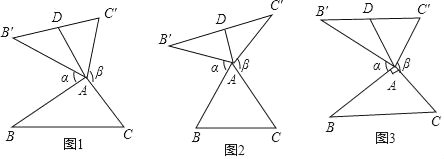
    （1）①如图2，当△ABC为等边三角形时，“旋补中线”AD与BC的数量关系为：AD＝　 　BC；

    ②如图3，当∠BAC＝90°，BC＝8时，则“旋补中线”AD长为　 　．

    （2）在图1中，当△ABC为任意三角形时，猜想“旋补中线”AD与BC的数量关系，并给予证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，直线与一次函数的图象交于点与反比例函数的图象交于点，点与点关于轴对称．

    （1）直接写出点的坐标；

    （2）求点的坐标（用含的式子表示）；

    （3）若两点中只有一个点在线段上，直接写出的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某工厂生产某种产品，每件产品的出厂价为50元，成本为25元．由于在生产过程中，平均每生产1件产品，有污水排出，所以为了净化环境，工厂设计两种方案对污水进行处理，并准备实施．

    方案甲：工厂将污水排到污水厂统一处理，每处理需付14元的排污费；

    方案乙：工厂将污水进行净化处理后再排出，每处理污水所用原料费为2元，且每月净化设备的损耗费为30000元．设工厂每月生产x件产品（x为正整数，）．

    （1）根据题意填写下表：

    每月生产产品的数量/件

    3500

    4500

    5500

    …

    方案甲处理污水的费用/元

    31500

    …

    方案乙处理污水的费用/元

    34500

    …

    （2）设工厂按方案甲处理污水时每月获得的利润为元，按方案乙处理污水时每月获得的利润为元，分别求，关于x的函数解析式；

    （3）根据题意填空：

    ①若该工厂按方案甲处理污水时每月获得的利润和按方案乙处理污水时每月获得利润相同，则该工厂每月生产产品的数量为_______件；

    ②若该工厂每月生产产品的数量为7500件时，则该工厂选用方案甲、方案乙中的方案_______处理污水时所获得的利润多；

    ③若该工厂每月获得的利润为81000元，则该工厂选用方案甲、方案乙中的方案________处理污水时生产产品的数量少．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，是半圆的直径，．射线为半圆的切线．在上取一点，连接交半圆于点，连接．过点作的垂线，垂足为点，与相交于点．过点作半圆的切线，切点为，与相交于点．

    （1）求证：∽；

    （2）当与的面积相等时，求的长；

    （3）求证：当在上移动时（点除外），点始终是线段的中点．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系xOy中，△ABC三个顶点坐标分别为A(-2，4)，B(-2，1)，C(-5，2)．

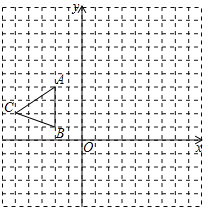
    （1）请画出△ABC关于x轴对称的△A1B1C1；

    （2）将△A1B1C1的三个顶点的横坐标与纵坐标同时乘-2，得到对应的点A2，B2，C2，请画出△A2B2C2；

    （3）△A1B1C1与△A2B2C2面积之比为 (不写解答过程，直接写出结果)．

    查看答案和解析>>

    同步练习册答案