
【题目】如图,△ABC中,∠BCA=90°,CD是边AB上的中线,分别过点C,D作BA和BC的平行线,两线交于点E,且DE交AC于点O,连接AE.

(1)求证:四边形ADCE是菱形;
(2)若∠B=60°,BC=6,求四边形ADCE的面积.
【答案】18![]()
【解析】
(1)欲证明四边形ADCE是菱形,需先证明四边形ADCE为平行四边形,然后再证明其对角线相互垂直;
(2)根据勾股定理得到AC的长度,由含30度角的直角三角形的性质求得DE的长度,然后由菱形的面积公式:S=![]() ACDE进行解答.
ACDE进行解答.
(1)证明:∵DE∥BC,EC∥AB,
∴四边形DBCE是平行四边形.
∴EC∥DB,且EC=DB.
在Rt△ABC中,CD为AB边上的中线,
∴AD=DB=CD.
∴EC=AD.
∴四边形ADCE是平行四边形.
∴ED∥BC.
∴∠AOD=∠ACB.
∵∠ACB=90°,
∴∠AOD=∠ACB=90°.
∴平行四边形ADCE是菱形;
(2)解:Rt△ABC中,CD为AB边上的中线,∠B=60°,BC=6,
∴AD=DB=CD=6.
∴AB=12,由勾股定理得AC=![]()
∵四边形DBCE是平行四边形,
∴DE=BC=6.
∴![]() =
=![]() =18
=18![]() .
.


科目:初中数学 来源: 题型:
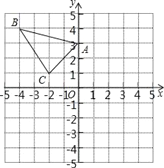
【题目】△ABC在直角坐标系内的位置如图所示.
(1)分别写出A、B、C的坐标;
(2)请在这个坐标系内画出△A1B1C1,使△A1B1C1与△ABC关于y轴对称,并写出B1的坐标;
(3)请在这个坐标系内画出△A2B2C2,使△A2B2C2与△ABC关于原点对称,并写出A2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李大妈加盟了“红红”全国烧烤连锁店,该公司的宗旨是“薄利多销”,经市场调查发现,当羊肉串的单价定为![]() 元时,每天能卖出
元时,每天能卖出![]() 串,在此基础上,每加价
串,在此基础上,每加价![]() 元李大妈每天就会少卖出
元李大妈每天就会少卖出![]() 串,考虑了所有因素后李大妈的每串羊肉串的成本价为
串,考虑了所有因素后李大妈的每串羊肉串的成本价为![]() 元,若李大妈每天销售这种羊肉串想获得利润是
元,若李大妈每天销售这种羊肉串想获得利润是![]() 元,那么请问这种羊肉串应怎样定价?
元,那么请问这种羊肉串应怎样定价?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC为等边三角形,D为AC的中点,∠EDF=120°,DE交线段AB于E,DF交直线BC于F.
(1)如图(1),求证:DE=DF;
(2)如图(2),若BE=3AE,求证:CF=![]() BC.
BC.
(3)如图(3),若BE=![]() AE,则CF= BC;在图(1)中,若BE=4AE,则CF= BC.
AE,则CF= BC;在图(1)中,若BE=4AE,则CF= BC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,BC=2AB,对角线相交于O,过C点作CE⊥BD交BD于E点,H为BC中点,连接AH交BD于G点,交EC的延长线于F点,下列5个结论:①EH=AB;②∠ABG=∠HEC;③△ABG≌△HEC;④S△GAD=S四边形GHCE,⑤CF=BD.正确的有( )个.

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次出数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() 、
、![]() 且
且![]() ,与
,与![]() 轴的正半轴的交点在
轴的正半轴的交点在![]() 的下方,则①
的下方,则①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() ,其中正确的个数为( )
,其中正确的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂在生产过程中要消耗大量电能,消耗每千度电产生利润与电价是一次函数关系,经过测算,工厂每千度电产生利润![]() (元/千度))与电价
(元/千度))与电价![]() (元/千度)的函数图象如图:
(元/千度)的函数图象如图:

![]() 当电价为
当电价为![]() 元/千度时,工厂消耗每千度电产生利润是多少?
元/千度时,工厂消耗每千度电产生利润是多少?
![]() 为了实现节能减排目标,有关部门规定,该厂电价
为了实现节能减排目标,有关部门规定,该厂电价![]() (元/千度)与每天用电量
(元/千度)与每天用电量![]() (千度)的函数关系为
(千度)的函数关系为![]() ,且该工厂每天用电量不超过
,且该工厂每天用电量不超过![]() 千度,为了获得最大利润,工厂每天应安排使用多少度电?工厂每天消耗电产生利润最大是多少元?
千度,为了获得最大利润,工厂每天应安排使用多少度电?工厂每天消耗电产生利润最大是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第二十四届冬季奥林匹克运动会将与2022年2月20日在北京举行,北京将成为历史上第一座举办过夏奥会又举办过冬奥会的城市,东宝区举办了一次冬奥会知识网上答题竞赛,甲、乙两校各有400名学生参加活动,为了解这两所学校的成绩情况,进行了抽样调查,过程如下,请补充完整.
(收集数据)
从甲、乙两校各随机抽取20名学生,在这次竞赛中它们的成绩如下:
甲 | 30 | 60 | 60 | 70 | 60 | 80 | 30 | 90 | 100 | 60 |
60 | 100 | 80 | 60 | 70 | 60 | 60 | 90 | 60 | 60 | |
乙 | 80 | 90 | 40 | 60 | 80 | 80 | 90 | 40 | 80 | 50 |
80 | 70 | 70 | 70 | 70 | 60 | 80 | 50 | 80 | 80 |
(整理、描述数据)按如下分数段整理、描述这两组样本数据:
(说明:优秀成绩为80<x≤100,良好成绩为50<x≤80,合格成绩为30≤x≤50.)
学校 | 平均分 | 中位数 | 众数 |
甲 | 67 | 60 | 60 |
乙 | 70 | 75 | a |
30≤x≤50 | 50<x≤80 | 80<x≤100 | |
甲 | 2 | 14 | 4 |
乙 | 4 | 14 | 2 |
(分析数据)两组样本数据的平均分、中位数、众数如右表所示:其中a= .
(得出结论)
(1)小伟同学说:“这次竞赛我得了70分,在我们学校排名属中游略偏上!”由表中数据可知小明是 校的学生;(填“甲”或“乙”)
(2)老师从乙校随机抽取一名学生的竞赛成绩,试估计这名学生的竞赛成绩为优秀的概率为 ;
(3)根据以上数据推断一所你认为竞赛成绩较好的学校,并说明理由.(至少从两个不同的角度说明推断的合理性)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正比例函数y=kx的图象经过点A,点A在第二象限.过点A作AH⊥x轴,垂足为H.已知点A的横坐标为﹣3,且△AOH的面积为4.5.
(1)求该正比例函数的解析式.
(2)将正比例函数y=kx向下平移,使其恰好经过点H,求平移后的函数解析式.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com