
【题目】已知二次出数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() 、
、![]() 且
且![]() ,与
,与![]() 轴的正半轴的交点在
轴的正半轴的交点在![]() 的下方,则①
的下方,则①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() ,其中正确的个数为( )
,其中正确的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】
根据已知画出图象,把x=-2代入得:4a-2b+c=0,2a+c=2b-2a;把x=-1代入得到a-b+c>0;根据-![]() <0,推出a<0,b<0,a+c>b,计算2a+c=2b-2a>0;代入得到2a-b+1=-
<0,推出a<0,b<0,a+c>b,计算2a+c=2b-2a>0;代入得到2a-b+1=-![]() c+1>0,根据结论判断即可.
c+1>0,根据结论判断即可.
根据二次函数y=ax2+bx+c的图象与x轴交于点(-2,0)、(x1,0),且1<x1<2,与y轴的正半轴的交点在(0,2)的下方,画出图象为:如图
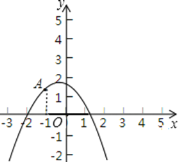
把x=-2代入得:4a-2b+c=0,∴①正确;
把x=-1代入得:y=a-b+c>0,又如图A点,a-b>-c<0,∴②不正确;
∵(-2,0)、(x1,0),且1<x1<2,
∴取符合条件1<x1<2的任何一个x1,-2x1<-2,
∴由一元二次方程根与系数的关系知 x1x2=![]() <-2,
<-2,
∴不等式的两边都乘以a(a<0)得:c>-2a,
∴2a+c>0,∴③正确;
④由4a-2b+c=0得 2a-b=-![]() ,
,
而0<c<2,∴-1<-<0
∴-1<2a-b<0
∴2a-b+1>0,
∴④正确.
所以①③④三项正确.
故选C.


科目:初中数学 来源: 题型:
【题目】我国是一个严重缺水的国家.为了加强公民的节水意识,某市制定了如下用水收费标准:每户每月的用水不超过6吨时,水价为每吨2元,超过6吨时,超过的部分按每吨3元收费.该市某户居民5月份用水x吨,应交水费y元.
(1)若0<x≤6,请写出y与x的函数关系式.
(2)若x>6,请写出y与x的函数关系式.
(3)在同一坐标系下,画出以上两个函数的图象.
(4)如果该户居民这个月交水费27元,那么这个月该户用了多少吨水?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() .
.

(1)先作![]() 的平分线交
的平分线交![]() 边于点
边于点![]() ,再以点
,再以点![]() 为圆心,
为圆心,![]() 长为半径作⊙
长为半径作⊙![]() .
.
(要求:尺规作图,保留作图痕迹,不写作法)
(2)请你判断(1)中![]() 与⊙
与⊙![]() 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.
(3)若![]() ,
,![]() ,求出(1)中⊙
,求出(1)中⊙![]() 的半径.
的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有下列说法:
①同一个人在相同的条件下做同一个实验,第一天做了![]() 次,第二天做了
次,第二天做了![]() 次,对这一实验中的同一事件来说,这两天出现的频率相等;
次,对这一实验中的同一事件来说,这两天出现的频率相等;
②投掷骰子,偶数朝上的概率是![]() ;
;
③如果一个袋里装有![]() 个红球,
个红球,![]() 个白球,从中任取
个白球,从中任取![]() 个,因为取出的球不是红球,就是白球,所以取出红球的概率是
个,因为取出的球不是红球,就是白球,所以取出红球的概率是![]() .
.
其中正确的有( )
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BCA=90°,CD是边AB上的中线,分别过点C,D作BA和BC的平行线,两线交于点E,且DE交AC于点O,连接AE.

(1)求证:四边形ADCE是菱形;
(2)若∠B=60°,BC=6,求四边形ADCE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为一座抛物线型的拱桥,AB、CD分别表示两个不同位置的水面宽度,O为拱桥顶部,水面AB宽为10米,AB距桥顶O的高度为12.5米,水面上升2.5米到达警戒水位CD位置时,水面宽为( )米.

A. 5 B. 2![]() C. 4
C. 4![]() D. 8
D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,过点A与x轴平行的直线交抛物线y=![]() 于点B、C,线段BC的长度为6,抛物线y=﹣2x2+b与y轴交于点A,则b=( )
于点B、C,线段BC的长度为6,抛物线y=﹣2x2+b与y轴交于点A,则b=( )
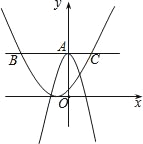
A. 1 B. 4.5 C. 3 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 为
为![]() 的直径,
的直径,![]() 、
、![]() 为
为![]() 的切线,
的切线,![]() 、
、![]() 为切点,
为切点,![]() 交
交![]() 于点
于点![]() ,
,![]() 的延长线交
的延长线交![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() .给出以下结论:①
.给出以下结论:①![]() ;②
;②![]() ;③点
;③点![]() 为
为![]() 的内心.其中正确的是________(填序号).
的内心.其中正确的是________(填序号).
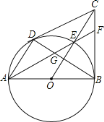
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在半圆O中,AB为直径,P为弧AB的中点,分别在弧AP和弧PB上取中点A1和B1,再在弧PA1和弧PB1上分别取中点A2和B2,若一直这样取中点,求∠AnPBn=__.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com