[题目]如图.在平面直角坐标系中.过点A与x轴平行的直线交抛物线y=于点B.C.线段BC的长度为6.抛物线y=﹣2x2+b与y轴交于点A.则b=( )A. 1 B. 4.5 C. 3 D. 6 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】如图，在平面直角坐标系中，过点A与x轴平行的直线交抛物线y=于点B、C，线段BC的长度为6，抛物线y=﹣2x2+b与y轴交于点A，则b=（　　）

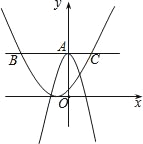
A. 1 B. 4.5 C. 3 D. 6

【答案】C

【解析】

根据题意知点A（0，b），设点C（x1，b）、点B（x2，b），则x1、x2是方程=b的两根，根据BC长度可得x1-x2=6即（x1+x2）2-4x1x2=36，由根与系数关系将x1+x2、x1x2代入求解可得．

根据题意点A（0，b），设点C（x1，b）、点B（x2，b），

抛物线y=中，当y=b时，有=b，

即：x2+2x+1﹣3b=0，

∴x1+x2=﹣2，x1x2=1﹣3b，

∵BC=6，即x1﹣x2=6，

∴（x1﹣x2）2=36，即（x1+x2）2﹣4x1x2=36，

则：4﹣4（1﹣3b）=36，

解得：b=3，

故选C．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】如图，边长为的正方形的对角线交于点，把边、分别绕点、同时逆时针旋转得四边形，其对角线交点为，连接．下列结论：

①四边形为菱形；

②；

③线段的长为；

④点运动到点的路径是线段．其中正确的结论共有（）

A. 1个 B. 2个 C. 3个 D. 4个

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】已知△ABC为等边三角形，D为AC的中点，∠EDF＝120°，DE交线段AB于E，DF交直线BC于F．

（1）如图（1），求证：DE＝DF；

（2）如图（2），若BE＝3AE，求证：CF＝BC．

（3）如图（3），若BE＝AE，则CF＝　　BC；在图（1）中，若BE＝4AE，则CF＝　　BC．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】已知二次出数的图象与轴交于点、且，与轴的正半轴的交点在的下方，则①，②，③，④，其中正确的个数为（）

A. 1个 B. 2个 C. 3个 D. 4个

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】某工厂在生产过程中要消耗大量电能，消耗每千度电产生利润与电价是一次函数关系，经过测算，工厂每千度电产生利润（元/千度））与电价（元/千度）的函数图象如图：

当电价为元/千度时，工厂消耗每千度电产生利润是多少？

为了实现节能减排目标，有关部门规定，该厂电价（元/千度）与每天用电量（千度）的函数关系为，且该工厂每天用电量不超过千度，为了获得最大利润，工厂每天应安排使用多少度电？工厂每天消耗电产生利润最大是多少元？

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】设双曲线与直线交于A，B两点（点A在第三象限），将双曲线在第一象限的一支沿射线BA的方向平移，使其经过点A，将双曲线在第三象限的一支沿射线AB的方向平移，使其经过点B，平移后的两条曲线相交于P，Q两点，此时我们称平移后的两条曲线所围部分（如图中阴影部分）为双曲线的“眸”，PQ为双曲线的“眸径”，当双曲线的眸径为9时，的值为_____．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】第二十四届冬季奥林匹克运动会将与2022年2月20日在北京举行，北京将成为历史上第一座举办过夏奥会又举办过冬奥会的城市，东宝区举办了一次冬奥会知识网上答题竞赛，甲、乙两校各有400名学生参加活动，为了解这两所学校的成绩情况，进行了抽样调查，过程如下，请补充完整．

（收集数据）

从甲、乙两校各随机抽取20名学生，在这次竞赛中它们的成绩如下：

甲	30	60	60	70	60	80	30	90	100	60
	60	100	80	60	70	60	60	90	60	60
乙	80	90	40	60	80	80	90	40	80	50
	80	70	70	70	70	60	80	50	80	80

（整理、描述数据）按如下分数段整理、描述这两组样本数据：

（说明：优秀成绩为80＜x≤100，良好成绩为50＜x≤80，合格成绩为30≤x≤50．）

学校	平均分	中位数	众数
甲	67	60	60
乙	70	75	a

	30≤x≤50	50＜x≤80	80＜x≤100
甲	2	14	4
乙	4	14	2

（分析数据）两组样本数据的平均分、中位数、众数如右表所示：其中a=　　．

（得出结论）

（1）小伟同学说：“这次竞赛我得了70分，在我们学校排名属中游略偏上！”由表中数据可知小明是　　校的学生；（填“甲”或“乙”）

（2）老师从乙校随机抽取一名学生的竞赛成绩，试估计这名学生的竞赛成绩为优秀的概率为　　；

（3）根据以上数据推断一所你认为竞赛成绩较好的学校，并说明理由．（至少从两个不同的角度说明推断的合理性）

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】已知：如图，在梯形ABCD中，AB∥CD，∠D=90°，AD=CD=2，点E在边AD上（不与点A、D重合），∠CEB=45°，EB与对角线AC相交于点F，设DE=x．

（1）用含x的代数式表示线段CF的长；

（2）如果把△CAE的周长记作C△CAE，△BAF的周长记作C△BAF，设=y，求y关于x的函数关系式，并写出它的定义域；

（3）当∠ABE的正切值是时，求AB的长．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，已知⊙O的半径为1，A,P,B,C是⊙O上的四个点，∠APC=∠CPB=60°

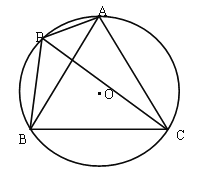
（1）当点P位于的什么位置时，四边形APBC的面积最大？并求出最大面积;

（2）试探究线段PA,PB,PC之间的数量关系，并证明你的结论．

查看答案和解析>>

同步练习册答案

甲	30	60	60	70	60	80	30	90	100	60
	60	100	80	60	70	60	60	90	60	60
乙	80	90	40	60	80	80	90	40	80	50
	80	70	70	70	70	60	80	50	80	80

甲	30	60	60	70	60	80	30	90	100	60
	60	100	80	60	70	60	60	90	60	60
乙	80	90	40	60	80	80	90	40	80	50
	80	70	70	70	70	60	80	50	80	80

练习册

高中

初中

小学

甲	30	60	60	70	60	80	30	90	100	60
	60	100	80	60	70	60	60	90	60	60
乙	80	90	40	60	80	80	90	40	80	50
	80	70	70	70	70	60	80	50	80	80