
【题目】如图,已知⊙O的半径为1,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°
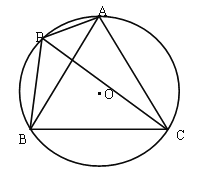
(1)当点P位于![]() 的什么位置时,四边形APBC的面积最大?并求出最大面积;
的什么位置时,四边形APBC的面积最大?并求出最大面积;
(2)试探究线段PA,PB,PC之间的数量关系,并证明你的结论.
【答案】(1)点P为![]() 的中点;
的中点;![]() .(2)CP=BP+AP.
.(2)CP=BP+AP.
【解析】
试题(1)过点P作PE⊥AB,垂足为E,过点C作CF⊥AB,垂足为F,把四边形的面积转化为两个三角形的面积进行计算,当点P为![]() 的中点时,PE+CF=PC从而得出最大面积.
的中点时,PE+CF=PC从而得出最大面积.
(2)在PC上截取PD=AP,则△APD是等边三角形,然后证明△APB≌△ADC,证明BP=CD,即可证得.
试题解析:(1)当点P为![]() 的中点时,四边形APBC的面积最大.
的中点时,四边形APBC的面积最大.
理由如下,如图1,过点P作PE⊥AB,垂足为E.
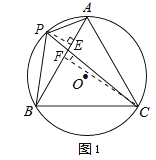
过点C作CF⊥AB,垂足为F.
∵![]()
∴S四边形APBC=![]() AB(PE+CF),
AB(PE+CF),
当点P为![]() 的中点时,PE+CF=PC,PC为⊙O的直径,
的中点时,PE+CF=PC,PC为⊙O的直径,
∴此时四边形APBC的面积最大.
又∵⊙O的半径为1,
∴其内接正三角形的边长AB=![]() ,
,
∴S四边形APBC=![]() ×2×
×2×![]() =
=![]() .
.
(2)在PC上截取PD=AP,如图2,
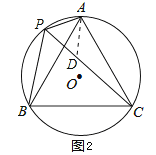
又∵∠APC=60°,
∴△APD是等边三角形,
∴AD=AP=PD,∠ADP=60°,即∠ADC=120°.
又∵∠APB=∠APC+∠BPC=120°,
∴∠ADC=∠APB,
在△APB和△ADC中,
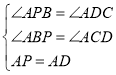 ,
,
∴△APB≌△ADC(AAS),
∴BP=CD,
又∵PD=AP,
∴CP=BP+AP.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,过点A与x轴平行的直线交抛物线y=![]() 于点B、C,线段BC的长度为6,抛物线y=﹣2x2+b与y轴交于点A,则b=( )
于点B、C,线段BC的长度为6,抛物线y=﹣2x2+b与y轴交于点A,则b=( )
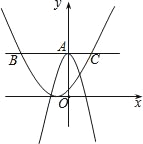
A. 1 B. 4.5 C. 3 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解九(1)班学生的体温情况,对这个班所有学生测量了一次体温(单位:℃),小明将测量结果绘制成如下统计表和如图所示的扇形统计图.下列说法错误的是( )
体温(℃) | 36.1 | 36.2 | 36.3 | 36.4 | 36.5 | 36.6 |
人数(人) | 4 | 8 | 8 | 10 | x | 2 |
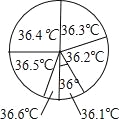
A.这些体温的众数是8
B.这些体温的中位数是36.35
C.这个班有40名学生
D.x=8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在半圆O中,AB为直径,P为弧AB的中点,分别在弧AP和弧PB上取中点A1和B1,再在弧PA1和弧PB1上分别取中点A2和B2,若一直这样取中点,求∠AnPBn=__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,点E在⊙O上,C为![]() 的中点,过点C作直线CD⊥AE于D,连接AC,BC.
的中点,过点C作直线CD⊥AE于D,连接AC,BC.

(1)试判断直线CD与⊙O的位置关系,并说明理由;
(2)若AD=2,AC=![]() ,求AB的长.
,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】这是某单位的平面示意图,已知大门的坐标为(-3,0),花坛的坐标为(0,-1).
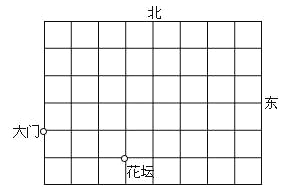
(1)根据上述条件建立平面直角坐标系;
(2)建筑物A的坐标为(3,1),请在图中标出A点的位置.
(3)建筑物B在大门北偏东45°的方向,并且B在花坛的正北方向处,请直接写出B点的坐标.
(4)在y轴上找一点C,使△ABC是以AB腰的等腰三角形,请直接写出点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水池的容积为90m3,水池中已有水10m3,现按8m3/h的流量向水池注水.
(1)写出水池中水的体积y(m3)与进水时间t(h)之间的函数表达式,并写出自变量t的取值范围;
(2)当t=1时,求y的值;当V=50时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个寻宝游戏的寻宝通道如图①所示,通道由在同一平面内的AB,BC,CA,OA, OB,OC组成。为记录寻宝者的行进路线,在BC的中点M处放置了一台定位仪器,设寻宝者行进的时间为x,寻宝者与定位仪器之间的距离为y,若寻宝者匀速行进,且表示y与x的函数关系的图像大致如图②所示,则寻宝者的行进路线可能为:

A. A→O→B B. B→A→C C. B→O→C D. C→B→O
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,直线y=﹣x+3与x轴、y轴交于点A,点B,点O关于直线AB的对称点为点O′,且点O′恰好在反比例函数y=![]() 的图象上.
的图象上.
(1)求点A与B的坐标;
(2)求k的值;
(3)若y轴正半轴有点P,过点P作x轴的平行线,且与反比例函数y=![]() 的图象交于点Q,设A、P、Q、O′四个点所围成的四边形的面积为S.若S=
的图象交于点Q,设A、P、Q、O′四个点所围成的四边形的面积为S.若S=![]() S△OAB时,求点P的坐标.
S△OAB时,求点P的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com