
【题目】已知:如图,直线y=﹣x+3与x轴、y轴交于点A,点B,点O关于直线AB的对称点为点O′,且点O′恰好在反比例函数y=![]() 的图象上.
的图象上.
(1)求点A与B的坐标;
(2)求k的值;
(3)若y轴正半轴有点P,过点P作x轴的平行线,且与反比例函数y=![]() 的图象交于点Q,设A、P、Q、O′四个点所围成的四边形的面积为S.若S=
的图象交于点Q,设A、P、Q、O′四个点所围成的四边形的面积为S.若S=![]() S△OAB时,求点P的坐标.
S△OAB时,求点P的坐标.

【答案】(1)A(3,0),B(0,3);(2)k的值为9;(3)P(0,2)或(0,6)
【解析】
(1)设A(a,0);B(0,b)代入即可求出a、b的值.进而求出A、B坐标.(2)如图① ,根据点O与O′关于直线AB对称,可知四边形OAO′B为正方形即可得答案.(3)设P(0,m),分两种情况:①当点P在点B的上方时,即:m>3,延长AO′于PQ相交于点M,设P(0,m),由面积关系可求;②当点P在点B的下方时,即:0<m<3,方法同上.
(1)设A(a,0);B(0,b),代入y=﹣x+3得:a=3,b=3,
所以A(3,0);B(0,3).
(2)如图①
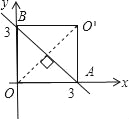
图①
∵点O与O′关于直线AB对称,
∴由题意可得四边形OAO′B为正方形,
∴O′(3,3)
则 k=3×3=9
即:k的值为9
(3)设P(0,m),显然,点P与点B不重合
①当点P在点B的上方时,即:m>3,
延长AO′于PQ相交于点M,如图②所示:

则:Q(![]() ,m),M(3,m)
,m),M(3,m)
∴PM=3,AM=m,MO′=m﹣3,QM=3﹣![]() ,
,
∴S=S△PMA﹣S△QMO′=![]() =
=![]() ×
×![]() =
=![]()
∴![]() ﹣
﹣![]() (3﹣m)(m+3)=
(3﹣m)(m+3)=![]() ,
,
解之得:m=6
②当点P在点B的下方时,即:0<m<3,如图③所示:
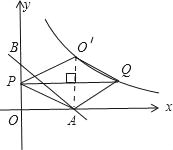
显然,PQ⊥AO′,
∴S=![]() PQAO′=
PQAO′=![]() ×3×
×3×![]() =
=![]() ,
,
∴m=2
∴P(0,2)或(0,6).


科目:初中数学 来源: 题型:
【题目】如图,已知⊙O的半径为1,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°
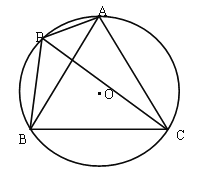
(1)当点P位于![]() 的什么位置时,四边形APBC的面积最大?并求出最大面积;
的什么位置时,四边形APBC的面积最大?并求出最大面积;
(2)试探究线段PA,PB,PC之间的数量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,等腰三角形ABC中,AB=AC,点D是BC的中点,DE⊥AB与点E、DF⊥AC与点F.求证:DE= DF;
(2)如图2,等腰三角形ABC中,AB=AC=13,BC=10,点D是BC边上的动点,DE⊥AB与点E、DF⊥AC与点F.请问DE+DF的值是否随点D位置的变化而变化?若不变,请直接写出DE+DF的值;若变化,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某旅行社为吸引市民组团去天水湾风景区旅游,推出如下收费标准:
![]() 如果人数不超过
如果人数不超过![]() 人,人均旅游费用为
人,人均旅游费用为![]() 元;
元;
![]() 如果人数超过
如果人数超过![]() 人,每增加
人,每增加![]() 人,人均旅游费用降低
人,人均旅游费用降低![]() 元,但人均旅游费用不得低于
元,但人均旅游费用不得低于![]() 元.
元.
某单位共付给该旅行社旅游费用![]() 元,问:该单位这次共有多少员工去天水湾风景区旅游?
元,问:该单位这次共有多少员工去天水湾风景区旅游?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 中,
中,![]() ,以
,以![]() 为直径的
为直径的![]() 交
交![]() 于
于![]() ,
,![]() 交
交![]() 于
于![]() ,
,![]() 交
交![]() 于
于![]() ,点
,点![]() 为
为![]() 延长线上的一点,
延长线上的一点,![]() 延长交
延长交![]() 于
于![]() ,
,![]() .小华得出
.小华得出![]() 个结论:①
个结论:①![]() ;②
;②![]() ;③
;③![]() .
.
其中正确的是( )

A. ①② B. ①③ C. ②③ D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点M,N分别是正方形ABCD的边BC,CD上的点,且BM=CN, AM与BN交于点P,试探索AM与BN的关系.
(1)数量关系_____________________,并证明;
(2)位置关系_____________________,并证明.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com