
【题目】如图,点M,N分别是正方形ABCD的边BC,CD上的点,且BM=CN, AM与BN交于点P,试探索AM与BN的关系.
(1)数量关系_____________________,并证明;
(2)位置关系_____________________,并证明.

【答案】(1)AM=BN,证明见解析;(2)AM⊥BN,证明见解析.
【解析】试题分析:(1)根据已知利用SAS证明△ABM≌△BCN即可得;
(2)由(1)中的三角形全等,从而得 ∠BAM=∠NBC,在△ABP中,利用三角形的内角和可得∠APB=90°,继而得到 AM⊥BN.
试题解析:(1)AM=BN,证明如下:
∵ 四边形ABCD是正方形,
∴ ∠ABM=∠BCN=90°,AB=BC
∵ BM=CN , ∴ △ABM≌△BCN ,∴ AM=BN;
(2)AM⊥BN,证明如下:
∵ △ABM≌△BCN, ∴ ∠BAM=∠NBC,
∵ ∠NBC+∠ABN=∠ABC=90°, ∴ ∠BAM+∠ABN=90°,
在△ABP中,∠APB=180°-(∠BAM+∠ABN)=90°,∴ AM⊥BN.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】某经销店为某工厂代销一种建筑材料(这里的代销是指厂家先免费提供货源,待货物售出后再进行结算,未售出的由厂家负责处理).当每吨售价为260元时,月销售量为45吨.该经销店为提高经营利润,准备采取降价的方式进行促销.经市场调查发现:当每吨售价每下降10元时,月销售量就会增加7.5吨.综合考虑各种因素,每售出一吨建筑材料共需支付厂家及其它费用100元.
(1)当每吨售价是240元时,计算此时的月销售量;
(2)若该经销店的月利润为9000元,则每吨材料售价为多少元?.
(3)该经销店要获得最大月利润,售价应定为每吨多少元;(直接写出答案即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线:y=ax2+bx+4与x轴交于点A(-2,0)和B(4,0)、与y轴交于点C.
(1)求抛物线的解析式;
(2)T是抛物线对称轴上的一点,且△ACT是以AC为底的等腰三角形,求点T的坐标;
(3)点M、Q分别从点A、B以每秒1个单位长度的速度沿x轴同时出发相向而行.当点M原点时,点Q立刻掉头并以每秒![]() 个单位长度的速度向点B方向移动,当点M到达抛物线的对称轴时,两点停止运动.过点M的直线l⊥轴,交AC或BC于点P.求点M的运动时间t(秒)与△APQ的面积S的函数关系式,并求出S的最大值.
个单位长度的速度向点B方向移动,当点M到达抛物线的对称轴时,两点停止运动.过点M的直线l⊥轴,交AC或BC于点P.求点M的运动时间t(秒)与△APQ的面积S的函数关系式,并求出S的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明从家去体育场锻炼,同时,妈妈从体育场以50米/分的速度回家,小明到体育场后发现要下雨,立即返回,追上妈妈后,小明以250米/分的速度回家取伞,立即又以250米/分的速度折回接妈妈,并一同回家.如图是两人离家的距离y(米)与小明出发的时间x(分)之间的函数图像.
(注:小明和妈妈始终在同一条笔直的公路上行走,图像上A、C、D三点在一条直线上)
(1)求线段BC的函数表达式;
(2)求点D坐标;
(3)当 x的值为 时,小明与妈妈相距1 500米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6,BC=8,将矩形ABCD沿CE折叠后,使点D恰好落在对角线AC上的点F处.
(1)求EF的长;
(2)求梯形ABCE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,△ABC的三个顶点坐标分别为A(0,4),B(2,4),C(3,﹣1).
(1)试在平面直角坐标系中,标出A、B、C三点;
(2)求△ABC的面积.
(3)若△A1B1C1与△ABC关于x轴对称,写出A1、B1、C1的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解西安市2018年中考数学学科各分数段成绩分布情况,从中抽取320名考生的中考数学成绩进行统计分析,在这个问题中,样本是指( )
A.320
B.抽取的320名考生
C.抽取的320名考生的中考数学成绩
D.西安市2018年中考数学成绩
查看答案和解析>>
科目:初中数学 来源: 题型:
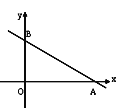
【题目】平面直角坐标系xOy中,点P的坐标为(a+1,a﹣1).
(1)试判断点P是否在一次函数y=x﹣2的图象上,并说明理由;
(2)如图,一次函数![]() 的图象与x轴、y轴分别相交于点A、B,若点P在△AOB的内部,求a的取值范围.
的图象与x轴、y轴分别相交于点A、B,若点P在△AOB的内部,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com