练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

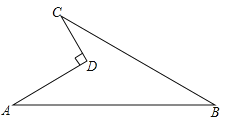
    【题目】如图所示的一块地，已知AD=4m，CD=3m，∠ADC=90°，AB=13m，BC=12m，求这块地的面积．

    【答案】24．

    【解析】试题分析：连接AC，利用勾股定理及逆定理可以得出三角形ACD和ABC是直角三角形，△ABC的面积减去△ACD的面积就是所求的面积．

    试题解析：解：连接AC ．

    在Rt△ACD中，AD=4，CD=3，∴AC 2 =AD 2 +CD 2 =4 2 +3 2 =25，又∵AC＞0，∴AC=5．

    又∵BC=12，AB=13，∴AC 2 +BC 2 =5 2 +12 2 =169，又∵AB 2 =169，∴AC 2 +BC 2 =AB 2 ，∴△ACB是直角三角形，∴S=S △ABC -S △ADC =30-6=24（m2）．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】下列多项式相乘，可以用平方差公式直接计算的是（ ）

    A. (x＋5y)(x－5y)B. (－x＋y)(y－x)

    C. (x＋3y)(2x－3y)D. (3x－2y)(2y－3x)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点M，N分别是正方形ABCD的边BC，CD上的点，且BM＝CN， AM与BN交于点P，试探索AM与BN的关系.

    （1）数量关系_____________________，并证明；

    （2）位置关系_____________________，并证明.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，一架2.5米长的梯子,斜靠在一竖直的墙上,这时梯足到墙底端的距离为0.7米,如果梯子的顶端沿墙下滑0.4米,那么梯足将向外移多少米?（5分）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算

    （1）5a5（-a）2-（-a4）（-2a）3

    （2）（a+b-c）（a-b-c）-（a-b+c）2

    （3）x（x-2y）-（y-x）2-（x+y）（-y+x）．

    （4）[x（x2y2-xy）-y（x2-x3y）]÷3x2y．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

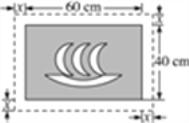
    【题目】在一幅长60 cm、宽40 cm的矩形风景画的四周镶一条金色纸边，制成一幅矩形挂图，如图所示，如果要使整个挂图的面积是2 816 cm2，设金色纸边的宽为x cm，那么x满足的方程是(　　)

    A. (60＋x)(40＋2x)＝2 816 B. (60＋x)(40＋x)＝2 816

    C. (60＋2x)(40＋x)＝2 816 D. (60＋2x)(40＋2x)＝2 816

    查看答案和解析>>

    科目：初中数学 来源： 题型：

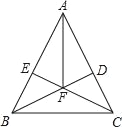
    【题目】如图，在△ABC中，AB=AC，BD⊥AC于D，CE⊥AB于E，BD、CE相交于F．

    求证：AF平分∠BAC．

    【答案】证明见解析.

    【解析】试题分析：先根据AB=AC，可得∠ABC=∠ACB，再由垂直，可得90°的角，在△BCE和△BCD中，利用内角和为180°，可分别求∠BCE和∠DBC，利用等量减等量差相等，可得FB=FC，再易证△ABF≌△ACF，从而证出AF平分∠BAC．

    试题解析：证明：∵AB=AC(已知)，

    ∴∠ABC=∠ACB(等边对等角).

    ∵BD、CE分别是高，

    ∴BD⊥AC,CE⊥AB(高的定义).

    ∴∠CEB=∠BDC=90°.

    ∴∠ECB=90°∠ABC,∠DBC=90°∠ACB.

    ∴∠ECB=∠DBC(等量代换).

    ∴FB=FC(等角对等边)，

    在△ABF和△ACF中，

    ，

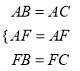    ∴△ABF≌△ACF(SSS)，

    ∴∠BAF=∠CAF(全等三角形对应角相等)，

    ∴AF平分∠BAC.

    【题型】解答题
    【结束】
    23

    【题目】如图，在△ABC中，AC=BC，∠C=90°，AD是△ABC的角平分线，DE⊥AB，垂足为E．

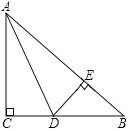
    （1）求证：CD=BE；

    （2）已知CD=2，求AC的长；

    （3）求证：AB=AC+CD．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】合肥百大集团新进了40台空调机，60台电冰箱，计划调配给下属的甲、乙两个连锁店销售，其中70台给甲连锁店，30台给乙连锁店．两个连锁店销售这两种电器每台的利润（元）如下表：

    空调机

    电冰箱

    甲连锁店

    200

    170

    乙连锁店

    160

    150

    设集团调配给甲连锁店x台空调机，集团卖出这100台电器的总利润为y（元）．

    （1）求y关于x的函数关系式，并求出x的取值范围；

    （2）为了促销，集团决定仅对甲连锁店的空调机每台让利a元销售，其他的销售利润不变，并且让利后每台空调机的利润仍然高于甲连锁店销售的每台电冰箱的利润，问该集团应该如何设计调配方案，才能使总利润达到最大？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知一个正数的平方根是a+3和2a-15．

    （1）求a的值；

    （2）求这个正数．

    查看答案和解析>>

    同步练习册答案