【题目】平面直角坐标系xOy中，点P的坐标为（a+1，a﹣1）．
（1）试判断点P是否在一次函数y=x﹣2的图象上，并说明理由；
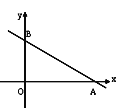
（2）如图，一次函数
的图象与x轴、y轴分别相交于点A、B，若点P在△AOB的内部，求a的取值范围．
全优点练单元计划系列答案科目：初中数学 来源： 题型：
【题目】如图，点M，N分别是正方形ABCD的边BC，CD上的点，且BM＝CN， AM与BN交于点P，试探索AM与BN的关系.
（1）数量关系_____________________，并证明；
（2）位置关系_____________________，并证明.
查看答案和解析>>
科目：初中数学 来源： 题型：
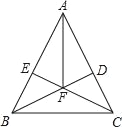
【题目】如图，在△ABC中，AB=AC，BD⊥AC于D，CE⊥AB于E，BD、CE相交于F．
求证：AF平分∠BAC．
【答案】证明见解析.
【解析】试题分析：先根据AB=AC，可得∠ABC=∠ACB，再由垂直，可得90°的角，在△BCE和△BCD中，利用内角和为180°，可分别求∠BCE和∠DBC，利用等量减等量差相等，可得FB=FC，再易证△ABF≌△ACF，从而证出AF平分∠BAC．
试题解析：证明：∵AB=AC(已知)，
∴∠ABC=∠ACB(等边对等角).
∵BD、CE分别是高，
∴BD⊥AC,CE⊥AB(高的定义).
∴∠CEB=∠BDC=90°.
∴∠ECB=90°∠ABC,∠DBC=90°∠ACB.
∴∠ECB=∠DBC(等量代换).
∴FB=FC(等角对等边)，
在△ABF和△ACF中，
，
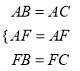∴△ABF≌△ACF(SSS)，
∴∠BAF=∠CAF(全等三角形对应角相等)，
∴AF平分∠BAC.
【题型】解答题
【结束】
23
【题目】如图，在△ABC中，AC=BC，∠C=90°，AD是△ABC的角平分线，DE⊥AB，垂足为E．
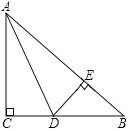
（1）求证：CD=BE；
（2）已知CD=2，求AC的长；
（3）求证：AB=AC+CD．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】合肥百大集团新进了40台空调机，60台电冰箱，计划调配给下属的甲、乙两个连锁店销售，其中70台给甲连锁店，30台给乙连锁店．两个连锁店销售这两种电器每台的利润（元）如下表：
空调机 | 电冰箱 | |
甲连锁店 | 200 | 170 |
乙连锁店 | 160 | 150 |
设集团调配给甲连锁店x台空调机，集团卖出这100台电器的总利润为y（元）．
（1）求y关于x的函数关系式，并求出x的取值范围；
（2）为了促销，集团决定仅对甲连锁店的空调机每台让利a元销售，其他的销售利润不变，并且让利后每台空调机的利润仍然高于甲连锁店销售的每台电冰箱的利润，问该集团应该如何设计调配方案，才能使总利润达到最大？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AB＝AC，AD是∠BAC的平分线，AE是∠BAC的外角平分线，ED∥AB交AC于点G.下列结论：①AD⊥AE；②AE∥BC；③AE＝AG；④AG＝
DE.正确的是________.(填序号)
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】据统计2017年5月深圳文博会期间，总参观人数达到了6 660 000人次，将6 660 000用科学记数法表示应为
A.666×104
B.6.66×105
C.6.66×106
D.6.66×107
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】新型冠状肺炎病毒(COVID﹣19)的粒子，其直径在120～140纳米即0.00000012米～0.00000014米之间，数据0.00000012用科学记数法可以表示为_____．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
