
【题目】如图,C在线段AB上,在AB的同侧作等边三角形△ACM和△BCN,连接AN,BM,若∠MBN=38°,则∠ANB=_____.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】为了解九(1)班学生的体温情况,对这个班所有学生测量了一次体温(单位:℃),小明将测量结果绘制成如下统计表和如图所示的扇形统计图.下列说法错误的是( )
体温(℃) | 36.1 | 36.2 | 36.3 | 36.4 | 36.5 | 36.6 |
人数(人) | 4 | 8 | 8 | 10 | x | 2 |
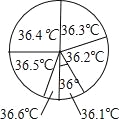
A.这些体温的众数是8
B.这些体温的中位数是36.35
C.这个班有40名学生
D.x=8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水池的容积为90m3,水池中已有水10m3,现按8m3/h的流量向水池注水.
(1)写出水池中水的体积y(m3)与进水时间t(h)之间的函数表达式,并写出自变量t的取值范围;
(2)当t=1时,求y的值;当V=50时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个寻宝游戏的寻宝通道如图①所示,通道由在同一平面内的AB,BC,CA,OA, OB,OC组成。为记录寻宝者的行进路线,在BC的中点M处放置了一台定位仪器,设寻宝者行进的时间为x,寻宝者与定位仪器之间的距离为y,若寻宝者匀速行进,且表示y与x的函数关系的图像大致如图②所示,则寻宝者的行进路线可能为:

A. A→O→B B. B→A→C C. B→O→C D. C→B→O
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC中,AB=AC,P点在BC边上的高AD上,且![]() ,BP的延长线交AC于E,若S△ABC=10,则S△ABE=_____;S△DEC=_____.
,BP的延长线交AC于E,若S△ABC=10,则S△ABE=_____;S△DEC=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题提出】
如图①,已知△ABC是等腰三角形,点E在线段AB上,点D在直线BC上,且ED=EC,将△BCE绕点C顺时针旋转60°至△ACF连接EF
试证明:AB=DB+AF
【类比探究】
(1)如图②,如果点E在线段AB的延长线上,其他条件不变,线段AB,DB,AF之间又有怎样的数量关系?请说明理由
(2)如果点E在线段BA的延长线上,其他条件不变,请在图③的基础上将图形补充完整,并写出AB,DB,AF之间的数量关系,不必说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,直线y=﹣x+3与x轴、y轴交于点A,点B,点O关于直线AB的对称点为点O′,且点O′恰好在反比例函数y=![]() 的图象上.
的图象上.
(1)求点A与B的坐标;
(2)求k的值;
(3)若y轴正半轴有点P,过点P作x轴的平行线,且与反比例函数y=![]() 的图象交于点Q,设A、P、Q、O′四个点所围成的四边形的面积为S.若S=
的图象交于点Q,设A、P、Q、O′四个点所围成的四边形的面积为S.若S=![]() S△OAB时,求点P的坐标.
S△OAB时,求点P的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com