
【题目】【问题提出】
如图①,已知△ABC是等腰三角形,点E在线段AB上,点D在直线BC上,且ED=EC,将△BCE绕点C顺时针旋转60°至△ACF连接EF
试证明:AB=DB+AF
【类比探究】
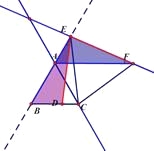
(1)如图②,如果点E在线段AB的延长线上,其他条件不变,线段AB,DB,AF之间又有怎样的数量关系?请说明理由
(2)如果点E在线段BA的延长线上,其他条件不变,请在图③的基础上将图形补充完整,并写出AB,DB,AF之间的数量关系,不必说明理由.

【答案】证明见解析;(1)AB=BD﹣AF;(2)AF=AB+BD.
【解析】试题分析:(1)根据旋转的性质得出△EDB与FEA全等的条件BE=AF,再结合已知条件和旋转的性质推出∠D=∠AEF,∠EBD=∠EAF=120°,得出△EDB≌FEA,所以BD=AF,等量代换即可得出结论.(2)先画出图形证明∴△DEB≌△EFA,方法类似于(1);(3)画出图形根据图形直接写出结论即可.
试题解析:(1)证明:DE=CE=CF,△BCE
由旋转60°得△ACF,
∴∠ECF=60°,BE=AF,CE=CF,
∴△CEF是等边三角形,
∴EF=CE,
∴DE=EF,∠CAF=∠BAC=60°,
∴∠EAF=∠BAC+∠CAF=120°,
∵∠DBE=120°,
∴∠EAF=∠DBE,
又∵A,E,C,F四点共圆,
∴∠AEF=∠ACF,
又∵ED=DC,
∴∠D=∠BCE,∠BCE=∠ACF,
∴∠D=∠AEF,
∴△EDB≌FEA,
∴BD=AF,AB=AE+BF,
∴AB=BD+AF.
类比探究(1)DE=CE=CF,△BCE由旋转60°得△ACF,
∴∠ECF=60°,BE=AF,CE=CF,
∴△CEF是等边三角形,
∴EF=CE,
∴DE=EF,∠EFC=∠BAC=60°,
∠EFC=∠FGC+∠FCG,∠BAC=∠FGC+∠FEA,
∴∠FCG=∠FEA,
又∠FCG=∠EAD
∠D=∠EAD,
∴∠D=∠FEA,
由旋转知∠CBE=∠CAF=120°,
∴∠DBE=∠FAE=60°
∴△DEB≌△EFA,
∴BD=AE, EB=AF,
∴BD=FA+AB.
即AB=BD-AF.
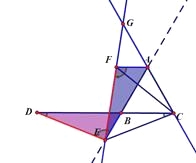
(2)AF=BD+AB(或AB=AF-BD)


科目:初中数学 来源: 题型:
【题目】如图,一次函数y=-![]() x+4的图象与x轴和y轴分别交于点A和B,再将△AOB沿直线CD对折,使点A与点B重合、直线CD与x轴交于点C,与AB交于点D.
x+4的图象与x轴和y轴分别交于点A和B,再将△AOB沿直线CD对折,使点A与点B重合、直线CD与x轴交于点C,与AB交于点D.

(1)点A的坐标为_________,点B的坐标为_________;
(2)在直线AB上是否存在点P使得△APO的面积为12?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由;
(3)求OC的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图的正方形网格中,每一个小正方形的边长均为 1.格点三角形 ABC(顶点是网格线交点的三角形)的顶点 A、C 的坐标分别是(﹣2,0),(﹣3,3).
(1)请在图中的网格平面内建立平面直角坐标系,写出点 B 的坐标;
(2)把△ABC 绕坐标原点 O 顺时针旋转 90°得到△A1B1C1,画出△A1B1C1,写出点
B1的坐标;
(3)以坐标原点 O 为位似中心,相似比为 2,把△A1B1C1 放大为原来的 2 倍,得到△A2B2C2 画出△A2B2C2,使它与△AB1C1 在位似中心的同侧;
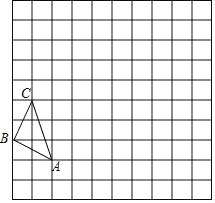
请在 x 轴上求作一点 P,使△PBB1 的周长最小,并写出点 P 的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ABC中,AB=AC,∠B=36°,D、E是BC上两点,且∠ADE=∠AED=2∠BAD,则图中等腰三角形共有( )

A.3个B.4个C.5个D.6个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如图的折线图,则符合这一结果的实验最有可能的是( )

A. 在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
B. 掷一枚质地均匀的正六面体骰子,向上一面的点数是4
C. 一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌,抽中红桃
D. 抛掷一枚均匀的硬币,前2次都正面朝上,第3次正面仍朝上
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某旅行社为吸引市民组团去天水湾风景区旅游,推出如下收费标准:
![]() 如果人数不超过
如果人数不超过![]() 人,人均旅游费用为
人,人均旅游费用为![]() 元;
元;
![]() 如果人数超过
如果人数超过![]() 人,每增加
人,每增加![]() 人,人均旅游费用降低
人,人均旅游费用降低![]() 元,但人均旅游费用不得低于
元,但人均旅游费用不得低于![]() 元.
元.
某单位共付给该旅行社旅游费用![]() 元,问:该单位这次共有多少员工去天水湾风景区旅游?
元,问:该单位这次共有多少员工去天水湾风景区旅游?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面内有一等腰Rt△ABC,∠ACB=90°,点A在直线l上.过点C作CE⊥1于点E,过点B作BF⊥l于点F,测量得CE=3,BF=2,则AF的长为( )

A. 5 B. 4 C. 8 D. 7
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com