
【题目】如图所示,△ABC中,AB=AC,∠B=36°,D、E是BC上两点,且∠ADE=∠AED=2∠BAD,则图中等腰三角形共有( )

A.3个B.4个C.5个D.6个
【答案】D
【解析】
根据等边对等角求出∠C,再根据三角形的内角和定理求出∠ADE,∠AED,∠BAD的度数,然后根据三角形的一个外角等于与它不相邻的两个内角的和求出∠EAD,∠CAE的度数,从而得到相等的角,根据相等的角找出等腰三角形即可得解.
解:∵AB=AC,∠B=36°,
∴∠C=∠B=36°,
∵∠ADE=∠AED=2∠BAD,
∵∠ADE=∠B+∠BAD,
∴∠B=∠BAD=36°,
∴∠ADE=∠AED=72°,
∴∠DAE=36°,
∴∠CAE=∠AED﹣∠C=72°﹣36°=36°,
∴∠BAE=∠CAD=36°+36°=72°,
等腰三角形有:△ABD、△ADE、△ACE、△ABE、△ACD、△ABC共6个.
故选:D.


科目:初中数学 来源: 题型:
【题目】某批发门市销售两种商品,甲种商品每件售价为300元,乙种商品每件售价为80元.新年来临之际,该门市为促销制定了两种优惠方案:
方案一:买一件甲种商品就赠送一件乙种商品;
方案二:按购买金额打八折付款.
某公司为奖励员工,购买了甲种商品20件,乙种商品x(x≥20)件.
(1)分别写出优惠方案一购买费用y1(元)、优惠方案二购买费用y2(元)与所买乙种商品x(件)之间的函数关系式;
(2)若该公司共需要甲种商品20件,乙种商品40件.设按照方案一的优惠办法购买了m件甲种商品,其余按方案二的优惠办法购买.请你写出总费用w与m之间的关系式;利用w与m之间的关系式说明怎样购买最实惠.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】这是某单位的平面示意图,已知大门的坐标为(-3,0),花坛的坐标为(0,-1).
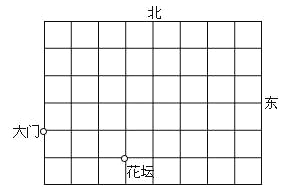
(1)根据上述条件建立平面直角坐标系;
(2)建筑物A的坐标为(3,1),请在图中标出A点的位置.
(3)建筑物B在大门北偏东45°的方向,并且B在花坛的正北方向处,请直接写出B点的坐标.
(4)在y轴上找一点C,使△ABC是以AB腰的等腰三角形,请直接写出点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A,B,C在数轴上对应的数分别为1,3,5,点P在数轴上对应的数是﹣2.点P关于点A的对称点为P1,点P1关于点B的对称点为P2,点P2关于点C的对称点为P3,点P3关于点A的对称点为P4,…则P1P2018的长为_____.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个寻宝游戏的寻宝通道如图①所示,通道由在同一平面内的AB,BC,CA,OA, OB,OC组成。为记录寻宝者的行进路线,在BC的中点M处放置了一台定位仪器,设寻宝者行进的时间为x,寻宝者与定位仪器之间的距离为y,若寻宝者匀速行进,且表示y与x的函数关系的图像大致如图②所示,则寻宝者的行进路线可能为:

A. A→O→B B. B→A→C C. B→O→C D. C→B→O
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形OABC中,OA=3,OC=2,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数y=![]() (k>0)的图象与BC边交于点E.
(k>0)的图象与BC边交于点E.
(1)当F为AB的中点时,求该函数的解析式;
(2)当k为何值时,△EFA的面积为![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题提出】
如图①,已知△ABC是等腰三角形,点E在线段AB上,点D在直线BC上,且ED=EC,将△BCE绕点C顺时针旋转60°至△ACF连接EF
试证明:AB=DB+AF
【类比探究】
(1)如图②,如果点E在线段AB的延长线上,其他条件不变,线段AB,DB,AF之间又有怎样的数量关系?请说明理由
(2)如果点E在线段BA的延长线上,其他条件不变,请在图③的基础上将图形补充完整,并写出AB,DB,AF之间的数量关系,不必说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,直线AB:y=x+b交y轴于点A(0,4),交x轴于点B.

(1)求点B的坐标;
(2)直线l垂直平分OB交AB于点D,交x轴于点E,点P是直线l上一动点,且在点D的上方,设点P的纵坐标为n.
①用含n的代数式表示△ABP的面积;
②当S△ABP=8时,求点P的坐标;
(3)在(2)中②的条件下,以PB为斜边作等腰直角△PBC,求点C的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如下图,在平面直角坐标系中,点A的坐标为(0,4),点B的坐标为(3,0),

(1)在图中作出线段AB以二四象限的角平分线为对称轴的对称线段CD,并直接写出四边形ABDC的面积为 ;
(2)若点C为格点(横纵坐标均为整数),且AB⊥OC,且AB=OC,作出线段OC;并写出C点坐标为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com