Question

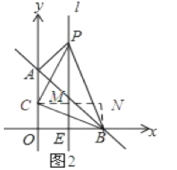
【题目】如图,平面直角坐标系中,直线AB:y=x+b交y轴于点A(0,4)，交x轴于点B.

(1)求点B的坐标；

(2)直线l垂直平分OB交AB于点D，交x轴于点E，点P是直线l上一动点，且在点D的上方，设点P的纵坐标为n.

①用含n的代数式表示△ABP的面积；

②当S△ABP=8时，求点P的坐标；

(3)在(2)中②的条件下，以PB为斜边作等腰直角△PBC，求点C的坐标。

Answer 1

【答案】（1）(4,0)；（2）①S△ABP =2n4.；②(2,6)；（3）(6,4)或(0,2)

【解析】

（1）把点A的坐标代入直线解析式可求得b=4，则直线的解析式为y=-x+4，令y=0可求得x=4，故此可求得点B的坐标；

（2）①由题l垂直平分OB可知OE=BE=2，将x=2代入直线AB的解析式可求得点D的坐标，设点P的坐标为（2，n），然后依据S△APB=S△APD+S△BPD可得到△APB的面积与n的函数关系式为S△APB=2n-4；

②由S△ABP=8得到关于n的方程可求得n的值，从而得到点P的坐标；

③如图1所示，过点C作CM⊥l，垂足为M，再过点B作BN⊥CM于点N．设点C的坐标为（p，q），先证明△PCM≌△CBN，得到CM=BN，PM=CN，然后由CM=BN，PM=CN列出关于p、q的方程组可求得p、q的值；如图2所示，同理可求得点C的坐标．

(1)∵把A(0,4)代入y=x+b得b=4

∴直线AB的函数表达式为：y=x+4.

令y=0得：x+4=0，解得：x=4

∴点B的坐标为(4,0).

(2)①∵l垂直平分OB，

∴OE=BE=2.

∵将x=2代入y=x+4得：y=2+4=2.

∴点D的坐标为(2,2).

∵点P的坐标为(2,n)，

∴PD=n2.

∵S△APB=S△APD+S△BPD，

∴S△ABP= PDOE+PDBE= (n2)×2+ (n2)×2=2n4.

②∵S△ABP=8，

∴2n4=8，解得：n=6.

∴点P的坐标为(2,6).

（3）如图1所示：过点C作CM⊥l，垂足为M，再过点B作BN⊥CM于点N.

设点C(p,q).

∵△PBC为等腰直角三角形，PB为斜边，

∴PC=CB,∠PCM+∠MCB=90°.

∵CM⊥l，BN⊥CM，

∴∠PMC=∠BNC=90°,∠MPC+∠PCM=90°.

∴∠MPC=∠NCB.

在△PCM和△CBN中，

，

∴△PCM≌△CBN.

∴CM=BN，PM=CN.

∴ ,解得 .

∴点C的坐标为(6,4).

如图2所示：过点C作CM⊥l，垂足为M，再过点B作BN⊥CM于点N.

设点C(p,q).

∵△PBC为等腰直角三角形，PB为斜边，

∴PC=CB,∠PCM+∠MCB=90°.

∵CM⊥l，BN⊥CM，

∴∠PMC=∠BNC=90°,∠MPC+∠PCM=90°.

∴∠MPC=∠NCB.

在△PCM和△CBN中，

，

∴△PCM≌△CBN.

∴CM=BN，PM=CN.

∴ ,解得 .

∴点C的坐标为(0,2).

综上所述点C的坐标为(6,4)或(0,2).