
【题目】如图,一次函数y=-![]() x+4的图象与x轴和y轴分别交于点A和B,再将△AOB沿直线CD对折,使点A与点B重合、直线CD与x轴交于点C,与AB交于点D.
x+4的图象与x轴和y轴分别交于点A和B,再将△AOB沿直线CD对折,使点A与点B重合、直线CD与x轴交于点C,与AB交于点D.

(1)点A的坐标为_________,点B的坐标为_________;
(2)在直线AB上是否存在点P使得△APO的面积为12?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由;
(3)求OC的长度.
【答案】(1)(8,0),(0,4);(2)![]() (2,3);
(2,3);![]() (14,-3);(3)OC=3,
(14,-3);(3)OC=3,
【解析】
(1)令x=0和y=0即可求出点A,B的坐标;(2)设出点P的坐标,利用三角形的面积公式,分两种情况解答即可;(3)设出点C坐标,表示出BC,最后利用勾股定理即可求出OC.
解:(1)令x=0,则y=4,
∴B(0,4),
令y=0,则0=-![]() x+4,
x+4,
∴x=8,
∴A(8,0),
故答案为:(8,0),(0,4);
(2)设P(m,n),
∵A(8,0),O(0,0),∴AO=8
∴![]() =
=![]() ×AO×
×AO×![]() =12,即12=4
=12,即12=4![]() ,
,
∴n=±3,
当n=3时,3=-![]() m+4, ∴m=2, ∴
m+4, ∴m=2, ∴![]() (2,3);
(2,3);
当n=-3时,-3=-![]() m+4, ∴m=2, ∴
m+4, ∴m=2, ∴![]() (14,-3);
(14,-3);
∴存在符合条件的点为:![]() (2,3);
(2,3);![]() (14,-3);
(14,-3);
(3)设OC=a,
∴AC=8-a,
由折叠知,BC=AC=8-a,
在Rt△BOC中,OB=4,
根据勾股定理得,BC2-OC2=OB2,
∴(8-a)2-a2=16,
∴a=3,
即:OC=3,


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】有下列说法:
①同一个人在相同的条件下做同一个实验,第一天做了![]() 次,第二天做了
次,第二天做了![]() 次,对这一实验中的同一事件来说,这两天出现的频率相等;
次,对这一实验中的同一事件来说,这两天出现的频率相等;
②投掷骰子,偶数朝上的概率是![]() ;
;
③如果一个袋里装有![]() 个红球,
个红球,![]() 个白球,从中任取
个白球,从中任取![]() 个,因为取出的球不是红球,就是白球,所以取出红球的概率是
个,因为取出的球不是红球,就是白球,所以取出红球的概率是![]() .
.
其中正确的有( )
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
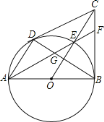
【题目】如图,已知![]() 为
为![]() 的直径,
的直径,![]() 、
、![]() 为
为![]() 的切线,
的切线,![]() 、
、![]() 为切点,
为切点,![]() 交
交![]() 于点
于点![]() ,
,![]() 的延长线交
的延长线交![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() .给出以下结论:①
.给出以下结论:①![]() ;②
;②![]() ;③点
;③点![]() 为
为![]() 的内心.其中正确的是________(填序号).
的内心.其中正确的是________(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某批发门市销售两种商品,甲种商品每件售价为300元,乙种商品每件售价为80元.新年来临之际,该门市为促销制定了两种优惠方案:
方案一:买一件甲种商品就赠送一件乙种商品;
方案二:按购买金额打八折付款.
某公司为奖励员工,购买了甲种商品20件,乙种商品x(x≥20)件.
(1)分别写出优惠方案一购买费用y1(元)、优惠方案二购买费用y2(元)与所买乙种商品x(件)之间的函数关系式;
(2)若该公司共需要甲种商品20件,乙种商品40件.设按照方案一的优惠办法购买了m件甲种商品,其余按方案二的优惠办法购买.请你写出总费用w与m之间的关系式;利用w与m之间的关系式说明怎样购买最实惠.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解九(1)班学生的体温情况,对这个班所有学生测量了一次体温(单位:℃),小明将测量结果绘制成如下统计表和如图所示的扇形统计图.下列说法错误的是( )
体温(℃) | 36.1 | 36.2 | 36.3 | 36.4 | 36.5 | 36.6 |
人数(人) | 4 | 8 | 8 | 10 | x | 2 |
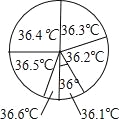
A.这些体温的众数是8
B.这些体温的中位数是36.35
C.这个班有40名学生
D.x=8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一巡查机器人接到指令,从原点O出发,沿O→A1→A2→A3→A4→A5→A6→A7→A8…的路线移动,每次移动1个单位长度,依次得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),A5(2,﹣1),A6(3,﹣1),A7(3,0),A8(4,0),…若机器人巡查到某一位置的横坐标为23时,即停止,则其纵坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在半圆O中,AB为直径,P为弧AB的中点,分别在弧AP和弧PB上取中点A1和B1,再在弧PA1和弧PB1上分别取中点A2和B2,若一直这样取中点,求∠AnPBn=__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】这是某单位的平面示意图,已知大门的坐标为(-3,0),花坛的坐标为(0,-1).
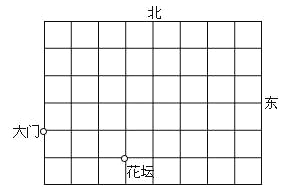
(1)根据上述条件建立平面直角坐标系;
(2)建筑物A的坐标为(3,1),请在图中标出A点的位置.
(3)建筑物B在大门北偏东45°的方向,并且B在花坛的正北方向处,请直接写出B点的坐标.
(4)在y轴上找一点C,使△ABC是以AB腰的等腰三角形,请直接写出点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题提出】
如图①,已知△ABC是等腰三角形,点E在线段AB上,点D在直线BC上,且ED=EC,将△BCE绕点C顺时针旋转60°至△ACF连接EF
试证明:AB=DB+AF
【类比探究】
(1)如图②,如果点E在线段AB的延长线上,其他条件不变,线段AB,DB,AF之间又有怎样的数量关系?请说明理由
(2)如果点E在线段BA的延长线上,其他条件不变,请在图③的基础上将图形补充完整,并写出AB,DB,AF之间的数量关系,不必说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com