Question

【题目】如图，，，，点在线段上，点在线段上，

（1）若，求四边形的面积；

（2）求证：

Answer 1

【答案】（1）50；（2）见解析

【解析】

（1）求出∠BAC=∠EAD，根据SAS推出△ABC≌△ADE，推出四边形ABCD的面积=三角形ACE的面积，即可得出答案；
（2）过点A作AG⊥CG，垂足为点G，求出AF=AG，求出CG=AG=GE，即可得出答案．

（1）∵∠BAD=∠CAE=90°，
∴∠BAC+∠CAD=∠EAD+∠CAD
∴∠BAC=∠EAD，
在△ABC和△ADE中，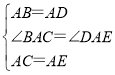
，
∴△ABC≌△ADE（SAS），
∵S四边形ABCD=S△ABC+S△ACD，
∴S四边形ABCD=S△ADE+S△ACD=S△ACE=×102=50；
（2）证明：∵△ACE是等腰直角三角形，
∴∠ACE=∠AEC=45°，
由△ABC≌△ADE得：
∠ACB=∠AEC=45°，
∴∠ACB=∠ACE，
∴AC平分∠ECF；
过点A作AG⊥CG，垂足为点G，

∵AC平分∠ECF，AF⊥CB，
∴AF=AG，
又∵AC=AE，
∴∠CAG=∠EAG=45°，
∴∠CAG=∠EAG=∠ACE=∠AEC=45°，
∴CG=AG=GE，
∴CE=2AG，
∴CE=2AF．