
【题目】已知△ABC为等边三角形,D为AC的中点,∠EDF=120°,DE交线段AB于E,DF交直线BC于F.
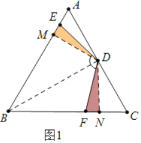
(1)如图(1),求证:DE=DF;
(2)如图(2),若BE=3AE,求证:CF=![]() BC.
BC.
(3)如图(3),若BE=![]() AE,则CF= BC;在图(1)中,若BE=4AE,则CF= BC.
AE,则CF= BC;在图(1)中,若BE=4AE,则CF= BC.

【答案】(1)证明见解析;(2)证明见解析;(3)![]() ,
,![]() .
.
【解析】
(1)如图1中,连接BD,作DM⊥AB于M,DN⊥BC于N,证明△DME≌△DNF即可得到结论;
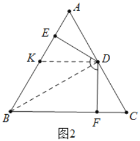
(2)如图2中,作DK∥BC交AB于K.设AE=a,则BE=3a,AB=AC=BC=4a,证明∠DFB=90°,求出CF即可解决问题;
(3)①如图3中,作DK∥BC交AB于K.只要证明△EDK≌△FDC,即可解决问题;
②如图4中,由(1)可知EM=FN,设AE=a,则BE=4a,AB=BC=AC=5a,AM=CN=![]() ,EM=FN=
,EM=FN=![]() a,可得CF=FN+CN=
a,可得CF=FN+CN=![]() a,由此即可 解决问题;
a,由此即可 解决问题;
证明:(1)如图1中,连接BD,作DM⊥AB于M,DN⊥BC于N,
∵∠DMB=∠DNB=90°,∠ABC=60°,
∴∠MDN=∠EDF=120°,
∴∠MDE=∠NDF,
∵△ABC是等边三角形,AD=DC,
∴∠DBA=∠DBC,
∴DM=DN,
∴△DME≌△DNF,
∴DE=DF.
(2)如图2中,作DK∥BC交AB于K.设AE=a,则BE=3a,AB=AC=BC=4a,
∵AD=DC,DK∥CB,
∴AK=BK=2a,DK=![]() BC=2a=AD=AK,
BC=2a=AD=AK,
∴AE=EK=a,
∴DE⊥AK,
∴∠BED=90°,
∵∠BED+∠BFD=180°,
∴∠DFB=90°,
在Rt△CDF中,∵∠C=60°,
∴CF=![]() CD=a,
CD=a,
∴CF=![]() BC.
BC.
(3)①如图3中,作DK∥BC交AB于K.
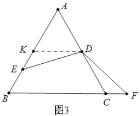
设BE=a,则AE=3a,AK=BK=2a,△ADK是等边三角形,
∴∠ADK=60°,∠EDF=∠KDC,
∴∠KDE=∠CDE,
∵DK=DC,DE=DF,
∴△EDK≌△FDC,
∴EK=CF=a,
∵BC=4a,
∴CF=![]() BC.
BC.
②如图4中,由(1)可知EM=FN,
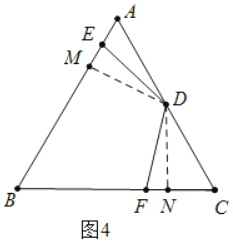
设AE=a,则BE=4a,AB=BC=AC=5a,AM=CN=![]() ,EM=FN=
,EM=FN=![]() a,
a,
∴CF=FN+CN=![]() a,
a,
∴CF:BC=![]() a:5a=3:10,
a:5a=3:10,
∴CF=![]() BC.
BC.
故答案为![]() ,
,![]() .
.


科目:初中数学 来源: 题型:
【题目】如图①所示,将两边AD与BC平行的纸条ABCD沿BD折叠,使点C落在C′处,AD与BC′相交于点E.

(1)求证:BE=DE;
(2)如图②,分别过点B,D作BM⊥AD,DN⊥BC′,垂足分别为M,N.求证:△BMD≌△DNB;
(3)若BM=4cm,DM=8cm,求ME的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AC=4,则四边形OCED的周长为( )

A. 4 B. 8 C. 10 D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() .
.

(1)先作![]() 的平分线交
的平分线交![]() 边于点
边于点![]() ,再以点
,再以点![]() 为圆心,
为圆心,![]() 长为半径作⊙
长为半径作⊙![]() .
.
(要求:尺规作图,保留作图痕迹,不写作法)
(2)请你判断(1)中![]() 与⊙
与⊙![]() 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.
(3)若![]() ,
,![]() ,求出(1)中⊙
,求出(1)中⊙![]() 的半径.
的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题12分)如图甲,在平面直角坐标系中,直线y=![]() x+8分别交x轴、y轴于点A、B,⊙O的半径为2
x+8分别交x轴、y轴于点A、B,⊙O的半径为2![]() 个单位长度.点P为直线y=
个单位长度.点P为直线y=![]() x+8上的动点,过点P作⊙O的切线PC、PD,切点分别为C、D,且PC⊥PD.
x+8上的动点,过点P作⊙O的切线PC、PD,切点分别为C、D,且PC⊥PD.

(1)试说明四边形OCPD的形状(要有证明过程);
(2)求点P的坐标;
(3)如图乙,若直线y=![]() x+b将⊙O的圆周分成两段弧长之比为1:3,请直接写出b的值
x+b将⊙O的圆周分成两段弧长之比为1:3,请直接写出b的值
(4)向右移动⊙O(圆心O始终保持在x轴上),试求出当⊙O与直线y=![]() x+8有交点时圆心O的横坐标m的取值范围。
x+8有交点时圆心O的横坐标m的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有下列说法:
①同一个人在相同的条件下做同一个实验,第一天做了![]() 次,第二天做了
次,第二天做了![]() 次,对这一实验中的同一事件来说,这两天出现的频率相等;
次,对这一实验中的同一事件来说,这两天出现的频率相等;
②投掷骰子,偶数朝上的概率是![]() ;
;
③如果一个袋里装有![]() 个红球,
个红球,![]() 个白球,从中任取
个白球,从中任取![]() 个,因为取出的球不是红球,就是白球,所以取出红球的概率是
个,因为取出的球不是红球,就是白球,所以取出红球的概率是![]() .
.
其中正确的有( )
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BCA=90°,CD是边AB上的中线,分别过点C,D作BA和BC的平行线,两线交于点E,且DE交AC于点O,连接AE.

(1)求证:四边形ADCE是菱形;
(2)若∠B=60°,BC=6,求四边形ADCE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,过点A与x轴平行的直线交抛物线y=![]() 于点B、C,线段BC的长度为6,抛物线y=﹣2x2+b与y轴交于点A,则b=( )
于点B、C,线段BC的长度为6,抛物线y=﹣2x2+b与y轴交于点A,则b=( )
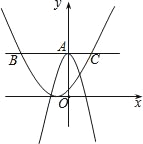
A. 1 B. 4.5 C. 3 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解九(1)班学生的体温情况,对这个班所有学生测量了一次体温(单位:℃),小明将测量结果绘制成如下统计表和如图所示的扇形统计图.下列说法错误的是( )
体温(℃) | 36.1 | 36.2 | 36.3 | 36.4 | 36.5 | 36.6 |
人数(人) | 4 | 8 | 8 | 10 | x | 2 |
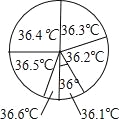
A.这些体温的众数是8
B.这些体温的中位数是36.35
C.这个班有40名学生
D.x=8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com