
【题目】如图①所示,将两边AD与BC平行的纸条ABCD沿BD折叠,使点C落在C′处,AD与BC′相交于点E.

(1)求证:BE=DE;
(2)如图②,分别过点B,D作BM⊥AD,DN⊥BC′,垂足分别为M,N.求证:△BMD≌△DNB;
(3)若BM=4cm,DM=8cm,求ME的长.
【答案】(1)见解析;(2)见解析;(3)3
【解析】
(1)根据平行线的性质可得:∠EDB=∠DBC,再根据折叠的性质可得:∠DBC=∠EBD,从而得出:∠EBD=∠EDB,由等角对等边可得:BE=DE;
(2)利用AAS即可证明△BME≌△DNE,从而得出BM=DN,再利用HL即可证出Rt△BMD≌Rt△DNB;
(3)由(1)中可知:BE=DE=DM﹣ME,再根据勾股定理列方程即可求出ME.
(1)证明:∵AD∥BC,
∴∠EDB=∠DBC,
∵将两边AD与BC平行的纸条ABCD沿BD折叠,使点C落在C′处,
∴∠DBC=∠EBD,
∴∠EBD=∠EDB,
∴BE=DE;
(2)证明:∵BM⊥AD,DN⊥BC′,
∴∠BME=∠DNE=90°,
在△BME与△DNE中,
 ,
,
∴△BME≌△DNE(AAS),
∴BM=DN,
在Rt△BMD与Rt△DNB中
![]() ,
,
∴Rt△BMD≌Rt△DNB(HL);
(3)解: ∵BM=4cm,DM=8cm,BE=DE
∴BE=DE=DM﹣ME=8﹣ME,
∴BM2+EM2=BE2,
即42+ME2=(8﹣ME)2,
∴ME=3.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某校八年级同学到距学校6千米的郊外秋游,一部分同学步行,另一部分同学骑自行车,沿相同路线前往,如图![]() 分别表示步行和骑车的同学前往目的地所走的路程y(千米)与所用时间
分别表示步行和骑车的同学前往目的地所走的路程y(千米)与所用时间![]() (分钟)之间的函数关系,则以下判断错误的是 ( )
(分钟)之间的函数关系,则以下判断错误的是 ( )

A.骑车的同学比步行的同学晚出发30分钟
B.骑车的同学比步行的同学早6分钟到达目的地
C.骑车的同学从出发到追上步行的同学用了20分钟
D.步行同学的速度是6千米/小时,骑车同学的速度是![]() 千米/小时.
千米/小时.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD中,AB=6,AC=3![]() ,将△ADC沿AC折叠,点D落在点D′处,CD′与AB交于点F.点P为线段AC(不含点A、C)上任意一点,PM⊥AB于点M,PN⊥CD′于点N,PM+PN=_____.
,将△ADC沿AC折叠,点D落在点D′处,CD′与AB交于点F.点P为线段AC(不含点A、C)上任意一点,PM⊥AB于点M,PN⊥CD′于点N,PM+PN=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△DEF中,满足AB=DE,∠B=∠E,如果要判定这两个三角形全等,那么添加的条件不正确的是( )

A. ∠A=∠D B. ∠C=∠F C. BC=EF D. AC=DF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是我国第24~30届奥运奖牌数的回眸和中国代表团奖牌总数统计图,根据表和统计图,以下描述正确的是( )
金牌(块) | 银牌(块) | 铜牌(块) | 总计奖牌数 | |
24 | 5 | 11 | 12 | 28 |
25 | 16 | 22 | 12 | 54 |
26 | 16 | 22 | 12 | 50 |
27 | 28 | 16 | 15 | 59 |
28 | 32 | 17 | 14 | 63 |
29 | 51 | 21 | 28 | 100 |
30 | 38 | 27 | 23 | 88 |

A.中国代表团的奥运奖牌总数一直保持上升趋势
B.折线统计图中的六条线段只是为了便于观察图象所反映的变化,不表示某种意思
C.与第29届北京奥运会相比,奥运金牌数、银牌数、铜牌数都有所下降
D.评价一个代表团在一届奥运会上的表现,我们只需关注金牌数,无需考虑其他
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在△ABC中,∠C=120°,边AC的垂直平分线DE与AC、AB分别交于点D和点E.
(1)作出边AC的垂直平分线DE;
(2)当AE=BC时,求∠A的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
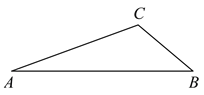
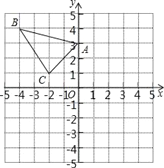
【题目】△ABC在直角坐标系内的位置如图所示.
(1)分别写出A、B、C的坐标;
(2)请在这个坐标系内画出△A1B1C1,使△A1B1C1与△ABC关于y轴对称,并写出B1的坐标;
(3)请在这个坐标系内画出△A2B2C2,使△A2B2C2与△ABC关于原点对称,并写出A2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为![]() 的正方形
的正方形![]() 的对角线交于点
的对角线交于点![]() ,把边
,把边![]() 、
、![]() 分别绕点
分别绕点![]() 、
、![]() 同时逆时针旋转
同时逆时针旋转![]() 得四边形
得四边形![]() ,其对角线交点为
,其对角线交点为![]() ,连接
,连接![]() .下列结论:
.下列结论:

①四边形![]() 为菱形;
为菱形;
②![]() ;
;
③线段![]() 的长为
的长为![]() ;
;
④点![]() 运动到点
运动到点![]() 的路径是线段
的路径是线段![]() .其中正确的结论共有( )
.其中正确的结论共有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC为等边三角形,D为AC的中点,∠EDF=120°,DE交线段AB于E,DF交直线BC于F.
(1)如图(1),求证:DE=DF;
(2)如图(2),若BE=3AE,求证:CF=![]() BC.
BC.
(3)如图(3),若BE=![]() AE,则CF= BC;在图(1)中,若BE=4AE,则CF= BC.
AE,则CF= BC;在图(1)中,若BE=4AE,则CF= BC.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com