
【题目】某工厂生产某种产品,每件产品的出厂价为50元,成本为25元.由于在生产过程中,平均每生产1件产品,有![]() 污水排出,所以为了净化环境,工厂设计两种方案对污水进行处理,并准备实施.
污水排出,所以为了净化环境,工厂设计两种方案对污水进行处理,并准备实施.
方案甲:工厂将污水排到污水厂统一处理,每处理![]() 需付14元的排污费;
需付14元的排污费;
方案乙:工厂将污水进行净化处理后再排出,每处理![]() 污水所用原料费为2元,且每月净化设备的损耗费为30000元.设工厂每月生产x件产品(x为正整数,
污水所用原料费为2元,且每月净化设备的损耗费为30000元.设工厂每月生产x件产品(x为正整数,![]() ).
).
(1)根据题意填写下表:
每月生产产品的数量/件 | 3500 | 4500 | 5500 | … |
方案甲处理污水的费用/元 | 31500 | … | ||
方案乙处理污水的费用/元 | 34500 | … |
(2)设工厂按方案甲处理污水时每月获得的利润为![]() 元,按方案乙处理污水时每月获得的利润为
元,按方案乙处理污水时每月获得的利润为![]() 元,分别求
元,分别求![]() ,
,![]() 关于x的函数解析式;
关于x的函数解析式;
(3)根据题意填空:
①若该工厂按方案甲处理污水时每月获得的利润和按方案乙处理污水时每月获得利润相同,则该工厂每月生产产品的数量为_______件;
②若该工厂每月生产产品的数量为7500件时,则该工厂选用方案甲、方案乙中的方案_______处理污水时所获得的利润多;
③若该工厂每月获得的利润为81000元,则该工厂选用方案甲、方案乙中的方案________处理污水时生产产品的数量少.
【答案】(1)24500,38500;33500,35500;(2)![]() ,
,![]() ;(3)①5000,②乙,③甲.
;(3)①5000,②乙,③甲.
【解析】
(1)根据污水量=产品数量×0.5立方米可求出该工厂污水排放量,按照甲乙方案分别计算处理污水的费用即可;
(2)每件产品出厂价为50,共![]() 件,则总收入为:
件,则总收入为:![]() ,成本费为
,成本费为![]() ,产生的污水总量为
,产生的污水总量为![]() ,按方案甲处理污水应花费:
,按方案甲处理污水应花费:![]() ,按方案乙处理应花费:
,按方案乙处理应花费:![]() .根据利润
.根据利润![]() 总收入
总收入![]() 总支出即可得到
总支出即可得到![]() 与
与![]() 的关系.
的关系.
(3)①当![]() 时,求出
时,求出![]() 的值即可;
的值即可;
②把![]() ,分别代入
,分别代入![]() ,
,![]() 求出函数值即可;
求出函数值即可;
②把![]() ,
,![]() 分别代入
分别代入![]() ,
,![]() 函数解析式分别求出x的值即可.
函数解析式分别求出x的值即可.
解:(1)当每月生产产品的数量3500件时,污水量=![]() (
(![]() )
)
方案甲费用为:![]() (元) ,方案乙费用为:
(元) ,方案乙费用为:![]() (元),
(元),
当每月生产产品的数量5500件时,污水量=![]() (
(![]() ),
),
方案甲费用为:![]() (元) ,方案乙费用为:
(元) ,方案乙费用为:![]() (元),
(元),
故答案为:24500,38500;33500,35500;
(2)根据题意,得![]() ,即
,即![]() ;
;
![]() ,即
,即![]()
(3)①依题意得:当![]() 时,即
时,即![]() ,解得:
,解得:![]() ,
,
②当![]() 时,
时,![]() (元);
(元);![]() ,
,
故方案乙利润多;
③工厂每月获得的利润为81000元,即![]() 时,
时,![]() ,解得
,解得![]() ;
;
当![]() 时,
时,![]() ,解得
,解得![]() ;
;
故方案甲生产产品的数量少;
故答案为:①5000;②乙;③甲.


科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连结BD、DP,BD与CF相交于点H,给出下列结论:①![]() ;②△DFP△BPH;③
;②△DFP△BPH;③![]() ; ④
; ④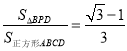 .其中正确的是______.(写出所有正确结论的序号).
.其中正确的是______.(写出所有正确结论的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2-4x+c(a≠0)与反比例函数y=![]() 的图象相交于B点,且B点的横坐标为3,抛物线与y轴交于点C(0,6),A是抛物线y=ax2-4x+c的顶点,P点是x轴上一动点,当PA+PB最小时,P点的坐标为_______.
的图象相交于B点,且B点的横坐标为3,抛物线与y轴交于点C(0,6),A是抛物线y=ax2-4x+c的顶点,P点是x轴上一动点,当PA+PB最小时,P点的坐标为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据规定,我市将垃圾分为了四类:可回收物、易腐垃圾、有害垃圾和其他垃圾四大类.现有投放这四类垃圾的垃圾桶各1个,若将用不透明垃圾袋分类打包好的两袋不同垃圾随机投进两个不同的垃圾桶,投放正确的概率是______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
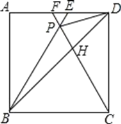
【题目】如图,已知半圆⊙O的直径AB=10,弦CD∥AB,且CD=8,E为弧CD的中点,点P在弦CD上,联结PE,过点E作PE的垂线交弦CD于点G,交射线OB于点F.
(1)当点F与点B重合时,求CP的长;
(2)设CP=x,OF=y,求y与x的函数关系式及定义域;
(3)如果GP=GF,求△EPF的面积.
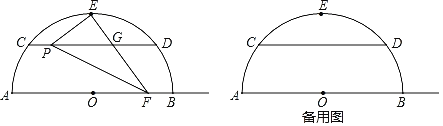
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为Rt△ABC直角边AC上一点,以OC为半径作⊙O与斜边AB相切于点D,交OA于点E,已知![]() ,AC=3,则图中阴影部分的面积是__________.
,AC=3,则图中阴影部分的面积是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
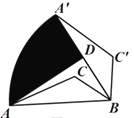
【题目】如图,在△ABC中,AB=4,若将△ABC绕点B顺时针旋转60°,点A的对应点为点A′,点C的对应点为点C′,点D为A′B的中点,连接AD.则点A的运动路径![]() 与线段AD、A′D围成的阴影部分面积是______.
与线段AD、A′D围成的阴影部分面积是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
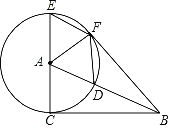
【题目】如图,在![]() ABC中,∠ACB=90°,以点A为圆心,AC的长为半径作⊙A,交AB于点D,交CA的延长线于点E.过点E作EF∥AB,交⊙A于点F,连接AF,BF,DF.
ABC中,∠ACB=90°,以点A为圆心,AC的长为半径作⊙A,交AB于点D,交CA的延长线于点E.过点E作EF∥AB,交⊙A于点F,连接AF,BF,DF.
(1)求证:BF是⊙A的切线;
(2)填空:
①当四边形ADFE是周长为20的菱形时,BF= ;
②当![]() = 时,四边形ACBF是正方形.
= 时,四边形ACBF是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
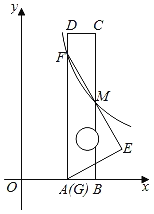
【题目】如图,将一把矩形直尺ABCD和一块含30°角的三角板EFG摆放在平面直角坐标系中,AB在x轴上,点G与点A重合,点F在AD上,三角板的直角边EF交BC于点M,反比例函数y=![]() (x>0)的图象恰好经过点F,M.若直尺的宽CD=3,三角板的斜边FG=
(x>0)的图象恰好经过点F,M.若直尺的宽CD=3,三角板的斜边FG=![]() ,则k=_____.
,则k=_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com