
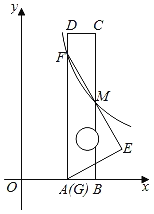
【题目】如图,将一把矩形直尺ABCD和一块含30°角的三角板EFG摆放在平面直角坐标系中,AB在x轴上,点G与点A重合,点F在AD上,三角板的直角边EF交BC于点M,反比例函数y=![]() (x>0)的图象恰好经过点F,M.若直尺的宽CD=3,三角板的斜边FG=
(x>0)的图象恰好经过点F,M.若直尺的宽CD=3,三角板的斜边FG=![]() ,则k=_____.
,则k=_____.
 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:
【题目】某工厂生产某种产品,每件产品的出厂价为50元,成本为25元.由于在生产过程中,平均每生产1件产品,有![]() 污水排出,所以为了净化环境,工厂设计两种方案对污水进行处理,并准备实施.
污水排出,所以为了净化环境,工厂设计两种方案对污水进行处理,并准备实施.
方案甲:工厂将污水排到污水厂统一处理,每处理![]() 需付14元的排污费;
需付14元的排污费;
方案乙:工厂将污水进行净化处理后再排出,每处理![]() 污水所用原料费为2元,且每月净化设备的损耗费为30000元.设工厂每月生产x件产品(x为正整数,
污水所用原料费为2元,且每月净化设备的损耗费为30000元.设工厂每月生产x件产品(x为正整数,![]() ).
).
(1)根据题意填写下表:
每月生产产品的数量/件 | 3500 | 4500 | 5500 | … |
方案甲处理污水的费用/元 | 31500 | … | ||
方案乙处理污水的费用/元 | 34500 | … |
(2)设工厂按方案甲处理污水时每月获得的利润为![]() 元,按方案乙处理污水时每月获得的利润为
元,按方案乙处理污水时每月获得的利润为![]() 元,分别求
元,分别求![]() ,
,![]() 关于x的函数解析式;
关于x的函数解析式;
(3)根据题意填空:
①若该工厂按方案甲处理污水时每月获得的利润和按方案乙处理污水时每月获得利润相同,则该工厂每月生产产品的数量为_______件;
②若该工厂每月生产产品的数量为7500件时,则该工厂选用方案甲、方案乙中的方案_______处理污水时所获得的利润多;
③若该工厂每月获得的利润为81000元,则该工厂选用方案甲、方案乙中的方案________处理污水时生产产品的数量少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地区为了加大“退耕还林”的力度,出台了一系列的激励措施:在“退耕还林”过程中,每一年的林地面积达到10亩且每年的林地面积在增加的农户,当年都可得生活补贴费2000元,且每超过10亩的部分还给予奖励每亩a元,在林间还有套种其他农作物,平均每亩还有b元的收入.
下表是某农户在头两年通过“退耕还林”每年获得的总收入情况:

(注:年总收入=生活补贴量+政府奖励量+种农作物收入)
(1)试根据以上提供的资料确定a、b的值.
(2)从2003年起,如果该农户每年新增林地的亩数比前一年按相同的增长率增长,那么2005年该农户获得的总收入达到多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,△ABC三个顶点坐标分别为A(-2,4),B(-2,1),C(-5,2).
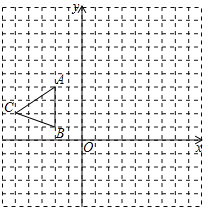
(1)请画出△ABC关于x轴对称的△A1B1C1;
(2)将△A1B1C1的三个顶点的横坐标与纵坐标同时乘-2,得到对应的点A2,B2,C2,请画出△A2B2C2;
(3)△A1B1C1与△A2B2C2面积之比为 (不写解答过程,直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】钟南山院士谈到防护新型冠状病毒肺炎时说:“我们需要重视防护,但也不必恐慌,尽量少去人员密集的场所,出门戴口罩,在室内注意通风,勤洗手,多运动,少熬夜.”某社区为了加强社区居民对新型冠状病毒肺炎防护知识的了解,通过微信群宣传新型冠状病毒肺炎的防护知识,并鼓励社区居民在线参与作答年新型冠状病毒防治全国统一考试全国卷试卷满分![]() 分,社区管理员随机从有
分,社区管理员随机从有![]() 人的某小区抽取
人的某小区抽取![]() 名人员的答卷成绩,根据他们的成绩数据绘制了如下的表格和统计图:
名人员的答卷成绩,根据他们的成绩数据绘制了如下的表格和统计图:
等级 | 成绩 | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
| |
根据上面提供的信息,回答下列问题: .
(1)统计表中的![]() ,
,![]() ,
,![]() ;
;
(2)请补全条形统计图;
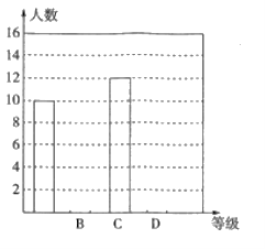
(3)根据抽样调查结果,请估计该小区答题成绩为“![]() 级”的有多少人?
级”的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
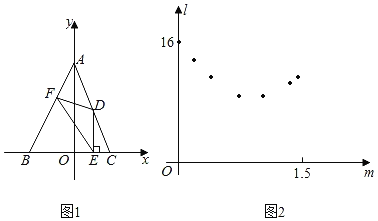
【题目】如图1,在平面直角坐标系中,△ABC的顶点A,C分別是直线y=﹣![]() x+4与坐标轴的交点,点B的坐标为(﹣2,0),点D是边AC上的一点,DE⊥BC于点E,点F在边AB上,且D,F两点关于y轴上的某点成中心对称,连结DF,EF.设点D的横坐标为m,EF2为l,请探究:
x+4与坐标轴的交点,点B的坐标为(﹣2,0),点D是边AC上的一点,DE⊥BC于点E,点F在边AB上,且D,F两点关于y轴上的某点成中心对称,连结DF,EF.设点D的横坐标为m,EF2为l,请探究:
①线段EF长度是否有最小值.
②△BEF能否成为直角三角形.
小明尝试用“观察﹣猜想﹣验证﹣应用”的方法进行探究,请你一起来解决问题.
(1)小明利用“几何画板”软件进行观察,测量,得到l随m变化的一组对应值,并在平面直角坐标系中以各对应值为坐标描点(如图2).请你在图2中连线,观察图象特征并猜想l与m可能满足的函数类别.
(2)小明结合图1,发现应用三角形和函数知识能验证(1)中的猜想,请你求出l关于m的函数表达式及自变量的取值范围,并求出线段EF长度的最小值.
(3)小明通过观察,推理,发现△BEF能成为直角三角形,请你求出当△BEF为直角三角形时m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是⊙O的直径,BA=BC,BD交AC于点E,点F在DB的延长线上,且∠BAF=∠C.
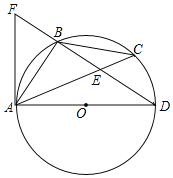
(1)求证:AF是⊙O的切线;
(2)若BC=2![]() ,BE=4,求⊙O半径r.
,BE=4,求⊙O半径r.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数![]() 和
和![]() 在第一象限内的图象如图所示,点P是
在第一象限内的图象如图所示,点P是![]() 的图象上一动点,作PC⊥x轴于点C,交
的图象上一动点,作PC⊥x轴于点C,交![]() 的图象于点A,作PD⊥y轴于点D,交
的图象于点A,作PD⊥y轴于点D,交![]() 的图象于点B,给出如下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积大小不会发生变化;④PA=3AC,其中正确的结论序号是( )
的图象于点B,给出如下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积大小不会发生变化;④PA=3AC,其中正确的结论序号是( )

A.①③B.②③④C.①③④D.①④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在坐标系中放置一菱形 OABC,已知∠ABC=60°,点 B 在 y 轴上,OA=1,先将菱形 OABC 沿 x 轴的正方向无滑动翻转,每次翻转 60°,连续翻转2019次,点 B 的落点依次为 B1,B2,B3,…,则 B2 019 的坐标为( )

A.(1010,0)B.(1310.5, ![]() )C.(1345,
)C.(1345, ![]() )D.(1346,0)
)D.(1346,0)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com