
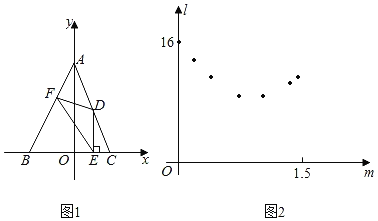
【题目】如图1,在平面直角坐标系中,△ABC的顶点A,C分別是直线y=﹣![]() x+4与坐标轴的交点,点B的坐标为(﹣2,0),点D是边AC上的一点,DE⊥BC于点E,点F在边AB上,且D,F两点关于y轴上的某点成中心对称,连结DF,EF.设点D的横坐标为m,EF2为l,请探究:
x+4与坐标轴的交点,点B的坐标为(﹣2,0),点D是边AC上的一点,DE⊥BC于点E,点F在边AB上,且D,F两点关于y轴上的某点成中心对称,连结DF,EF.设点D的横坐标为m,EF2为l,请探究:
①线段EF长度是否有最小值.
②△BEF能否成为直角三角形.
小明尝试用“观察﹣猜想﹣验证﹣应用”的方法进行探究,请你一起来解决问题.
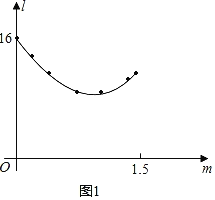
(1)小明利用“几何画板”软件进行观察,测量,得到l随m变化的一组对应值,并在平面直角坐标系中以各对应值为坐标描点(如图2).请你在图2中连线,观察图象特征并猜想l与m可能满足的函数类别.
(2)小明结合图1,发现应用三角形和函数知识能验证(1)中的猜想,请你求出l关于m的函数表达式及自变量的取值范围,并求出线段EF长度的最小值.
(3)小明通过观察,推理,发现△BEF能成为直角三角形,请你求出当△BEF为直角三角形时m的值.
【答案】(1)连线见解析,二次函数;(2)![]() ;(3)m=0或m=
;(3)m=0或m=![]()
【解析】
(1)根据描点法画图即可;
(2)过点F,D分别作FG,DH垂直于y轴,垂足分别为G,H,证明Rt△FGK≌Rt△DHK(AAS),由全等三角形的性质得出FG=DH,可求出F(﹣m,﹣2m+4),根据勾股定理得出l=EF2=8m2﹣16m+16=8(m﹣1)2+8,由二次函数的性质可得出答案;
(3)分三种不同情况,根据直角三角形的性质得出m的方程,解方程求出m的值,则可求出答案.
解:(1)用描点法画出图形如图1,由图象可知函数类别为二次函数.
(2)如图2,过点F,D分别作FG,DH垂直于y轴,垂足分别为G,H,
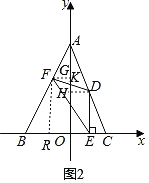
则∠FGK=∠DHK=90°,
记FD交y轴于点K,
∵D点与F点关于y轴上的K点成中心对称,
∴KF=KD,
∵∠FKG=∠DKH,
∴Rt△FGK≌Rt△DHK(AAS),
∴FG=DH,
∵直线AC的解析式为y=﹣![]() x+4,
x+4,
∴x=0时,y=4,
∴A(0,4),
又∵B(﹣2,0),
设直线AB的解析式为y=kx+b,
∴![]() ,
,
解得![]() ,
,
∴直线AB的解析式为y=2x+4,
过点F作FR⊥x轴于点R,
∵D点的橫坐标为m,
∴F(﹣m,﹣2m+4),
∴ER=2m,FR=﹣2m+4,
∵EF2=FR2+ER2,
∴l=EF2=8m2﹣16m+16=8(m﹣1)2+8,
令﹣![]() +4=0,得x=
+4=0,得x=![]() ,
,
∴0≤m≤![]() .
.
∴当m=1时,l的最小值为8,
∴EF的最小值为2![]() .
.
(3)①∠FBE为定角,不可能为直角.
②∠BEF=90°时,E点与O点重合,D点与A点,F点重合,此时m=0.
③如图3,∠BFE=90°时,有BF2+EF2=BE2.
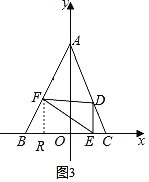
由(2)得EF2=8m2﹣16m+16,
又∵BR=﹣m+2,FR=﹣2m+4,
∴BF2=BR2+FR2=(﹣m+2)2+(﹣2m+4)2=5m2﹣20m+20,
又∵BE2=(m+2)2,
∴(5m2﹣20m+8)+(8m2﹣16m+16)2=(m+2)2,
化简得,3m2﹣10m+8=0,
解得m1=![]() ,m2=2(不合题意,舍去),
,m2=2(不合题意,舍去),
∴m=![]() .
.
综合以上可得,当△BEF为直角三角形时,m=0或m=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,O为Rt△ABC直角边AC上一点,以OC为半径作⊙O与斜边AB相切于点D,交OA于点E,已知![]() ,AC=3,则图中阴影部分的面积是__________.
,AC=3,则图中阴影部分的面积是__________.
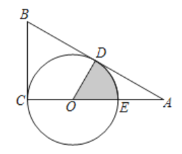
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据市卫生防疫部门的要求,游泳池必须定期换水后才能对外开放.在换水时需要经“排水一清冼一灌水”的过程.某游泳馆从早上![]() 开始对游泳池进行换水,已知该游泳池的排水速度是灌水速度的
开始对游泳池进行换水,已知该游泳池的排水速度是灌水速度的![]() 倍,其中游泳池内剩余的水量
倍,其中游泳池内剩余的水量![]() 与换水时间上
与换水时间上![]() 之间的函数图象如图所示,根据图象解答下列问题:
之间的函数图象如图所示,根据图象解答下列问题:
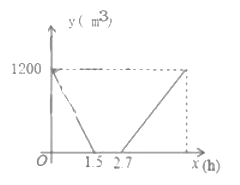
(1)该游泳池清洗需要 小时.
(2)求排水过程中的![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围.
的取值范围.
(3)若该游泳馆在换水结束![]() 分钟后才能对外开放,判断游泳爱好者小致能否在中午
分钟后才能对外开放,判断游泳爱好者小致能否在中午![]() 进入该游泳馆游泳,并说明理由.
进入该游泳馆游泳,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,以顶点
,以顶点![]() 为圆心,适当长为半径画弧,分别交边
为圆心,适当长为半径画弧,分别交边![]() 于点
于点![]() ;再分别以
;再分别以![]() 为圆心,以大于
为圆心,以大于![]() 为半径作弧,两弧在
为半径作弧,两弧在![]() 内交于点
内交于点![]() ;作射线
;作射线![]() 交边
交边![]() 于点
于点![]() 若
若![]() ,则
,则![]() 的面积为( )
的面积为( )
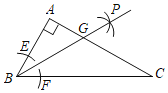
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
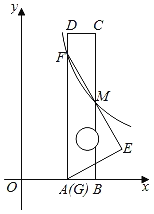
科目:初中数学 来源: 题型:
【题目】如图,将一把矩形直尺ABCD和一块含30°角的三角板EFG摆放在平面直角坐标系中,AB在x轴上,点G与点A重合,点F在AD上,三角板的直角边EF交BC于点M,反比例函数y=![]() (x>0)的图象恰好经过点F,M.若直尺的宽CD=3,三角板的斜边FG=
(x>0)的图象恰好经过点F,M.若直尺的宽CD=3,三角板的斜边FG=![]() ,则k=_____.
,则k=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解市民对“垃圾分类知识”的知晓程度,某数学学习兴趣小组对市民进行 随机抽样的问卷调查,调查结果分为“A.非常了解”、“B.了解”、“C.基本了解”、“D.不太了解”四个等级进行统计,并将统计结果绘制成如下两幅不完整的统计图(图1,图2), 请根据图中的信息解答下列问题.
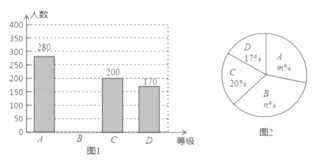
(1)这次调查的市民人数为________人,图2中,![]() _________;
_________;
(2)图1中的条形统计图中B等级的人数;
(3)在图2中的扇形统计图中,求“C.基本了解”所在扇形的圆心角度数;
(4)据统计,2018年该市约有市民500万人,那么根据抽样调查的结果,可估计对“垃圾分类知识”的知晓程度为“A.非常了解”的市民约有多少万人?
查看答案和解析>>
科目:初中数学 来源: 题型:
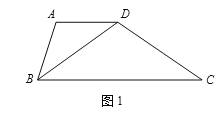
【题目】我们把有一组邻边相等,一组对边平行但不相等的四边形称作“准菱形”.
(1)证明“准菱形”性质:“准菱形”的一条对角线平分一个内角.
(要求:根据图1写出已知,求证,证明)
已知:
求证:
证明:
(2)已知.在△ABC中,∠A=90°,AB=3,AC=4.若点D,E分别在边BC,AC上,且四边形ABDE为“准菱形”.请在下列给出的△ABC中,作出满足条件的所有“准菱形”ABDE,并写出相应DE的长.(所给△ABC不一定都用,不够可添)
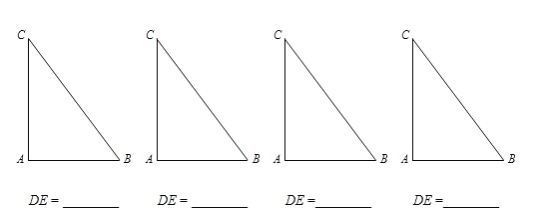
查看答案和解析>>
科目:初中数学 来源: 题型:
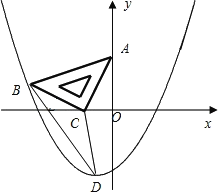
【题目】如图,在平面直角坐标系中,将一块腰长为![]() 的等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,直角顶点C的坐标为(1,0),点B在抛物线y=ax2+ax2上.
的等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,直角顶点C的坐标为(1,0),点B在抛物线y=ax2+ax2上.
(1)点A的坐标为 ,点B的坐标为 ;抛物线的解析式为 ;
(2)设抛物线的顶点为D,求△DBC的面积;
(3)在抛物线上是否还存在点P(点B除外),使△ACP仍然是以AC为直角边的等腰直角三角形?若存在,请直接写出所有点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】参照学习函数的过程方法,探究函数![]() 的图像与性质,因为
的图像与性质,因为![]() ,即
,即![]() ,所以我们对比函数
,所以我们对比函数![]() 来探究列表:
来探究列表:
| … | -4 | -3 | -2 | -1 |
|
| 1 | 2 | 3 | 4 | … | |
| … |
|
| 1 | 2 | 4 | -4 | -2 | -1 | <> |
| … | |
| … |
|
| 2 | 3 | 5 | -3 | -2 | 0 |
|
| … |
描点:在平面直角坐标系中以自变量![]() 的取值为横坐标,以
的取值为横坐标,以![]() 相应的函数值为纵坐标,描出相应的点如图所示:
相应的函数值为纵坐标,描出相应的点如图所示:
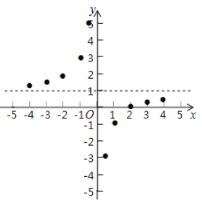
(1)请把![]() 轴左边各点和右边各点分别用一条光滑曲线,顺次连接起来;
轴左边各点和右边各点分别用一条光滑曲线,顺次连接起来;
(2)观察图象并分析表格,回答下列问题:
①当![]() 时,
时,![]() 随
随![]() 的增大而______;(“增大”或“减小”)
的增大而______;(“增大”或“减小”)
②![]() 的图象是由
的图象是由![]() 的图象向______平移______个单位而得到的;
的图象向______平移______个单位而得到的;
③图象关于点______中心对称.(填点的坐标)
(3)函数![]() 与直线
与直线![]() 交于点
交于点![]() ,
,![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com