
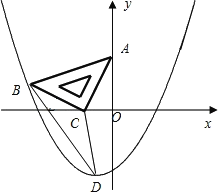
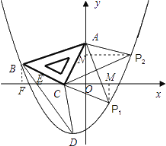
【题目】如图,在平面直角坐标系中,将一块腰长为![]() 的等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,直角顶点C的坐标为(1,0),点B在抛物线y=ax2+ax2上.
的等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,直角顶点C的坐标为(1,0),点B在抛物线y=ax2+ax2上.
(1)点A的坐标为 ,点B的坐标为 ;抛物线的解析式为 ;
(2)设抛物线的顶点为D,求△DBC的面积;
(3)在抛物线上是否还存在点P(点B除外),使△ACP仍然是以AC为直角边的等腰直角三角形?若存在,请直接写出所有点P的坐标;若不存在,请说明理由.
【答案】(1)A(0,2);B(![]() ,1);
,1);![]() (2)
(2)![]() (3)P(
(3)P(![]() ,
,![]() )或(2,1)
)或(2,1)
【解析】
(1)过点B作BF⊥x轴于F,先根据勾股定理求出OA的长,即可得出点A的坐标,再求出OF、BF的长即可求出B的坐标;再把点B的坐标代入抛物线的解析式,求出a的值,即可求出抛物线的解析式;
(2)先求出点D的坐标,再用待定系数法求出直线BD的解析式,设直线BD与x轴交点为E,求出CE的长,再根据S△DBC=S△CEB+S△CED进行计算即可;
(3)假设存在点P,①若以点C为直角顶点;则延长BC至点P1,使得P1C=BC,得到等腰直角三角形△ACP1,过点P1作P1M⊥x轴,由全等三角形的判定定理可得△MP1C≌△FBC,再由全等三角形的对应边相等可得出点P1点的坐标;
②若以点A为直角顶点;则过点A作AP2⊥CA,且使得AP2=AC,得到等腰直角三角形△ACP2,过点P2作P2N⊥y轴,同理可证△AP2N≌△CAO,由全等三角形的性质可得出点P2的坐标;点P1、P2的坐标代入抛物线的解析式进行检验即可.
(1)∵C(-1,0),AC=![]() ,
,
∴OA=![]() =2,
=2,
∴A(0,2);
过点B作BF⊥x轴于F,垂足为F,
∵∠ACO+∠CAO=90,∠ACO+∠BCF=90,
∴∠CAO=∠BCF,
在ΔAOC和ΔCFB中,
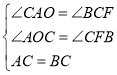 ,
,
∴ΔAOC≌ΔCFB,
∴CF=AO=2,BF=CO=1,
∴OF=3,
∴B(-3,1);
把B(-3,1)代入y=ax2+ax2中,得:1=9a-3a-2,
解得:a=![]() ,
,
∴抛物线的解析式为y=![]() x2+
x2+![]() x2,
x2,
故答案为:A(0,2);B(![]() ,1);
,1);![]() ;
;
(2)由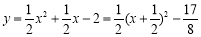 知,抛物线的顶点坐标D(
知,抛物线的顶点坐标D(![]() ,
,![]() ),
),
设直线BD的关系式为y=kx+b,将点B、D的坐标代入得:
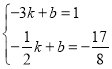 ,
,
解得: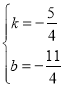 ,
,
∴直线BD的解析式为![]() ,设直线BD与x轴交于点E,
,设直线BD与x轴交于点E,
则点E(![]() ,0),CE=
,0),CE=![]() ,
,
∴S△DBC=S△CEB+S△CED=![]() =
=![]() ;
;
(3)假设存在点P,使得△ACP仍然是以AC为直角边的等腰直角三角形:
①若以点C为直角顶点;
则延长BC至点P1,使得P1C=BC,得到等腰直角三角形△ACP1,
过点P1作P1M⊥x轴,
∵CP1=BC,∠MCP1=∠BCF,∠P1MC=∠BFC=90 °,
∴△MP1C≌△FBC.
∴CM=CF=2,P1M=BF=1,
∴P1(1,-1);
②若以点A为直角顶点;
则过点A作AP2⊥CA,且使得AP2=AC,得到等腰直角三角形△ACP2,
过点P2作P2N⊥y轴,同理可证△AP2N≌△CAO,
∴NP2=OA=2,AN=OC=1,
∴P2(2,1),
经检验,点P1(1,-1)与点P2(2,1)都在抛物线![]() 上.
上.
综上所述,满足条件的P坐标为(![]() ,
,![]() )或(2,1).
)或(2,1).


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:
【题目】(1)问题发现
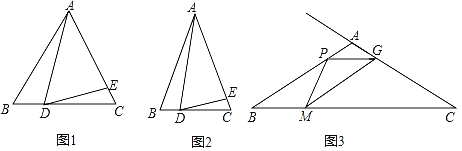
如图1,![]() ABC是等边三角形,点D,E分别在边BC,AC上,若∠ADE=60°,则AB,CE,BD,DC之间的数量关系是 .
ABC是等边三角形,点D,E分别在边BC,AC上,若∠ADE=60°,则AB,CE,BD,DC之间的数量关系是 .
(2)拓展探究
如图2,![]() ABC是等腰三角形,AB=AC,∠B=α,点D,E分别在边BC,AC上.若∠ADE=α,则(1)中的结论是否仍然成立?请说明理由.
ABC是等腰三角形,AB=AC,∠B=α,点D,E分别在边BC,AC上.若∠ADE=α,则(1)中的结论是否仍然成立?请说明理由.
(3)解决问题
如图3,在![]() ABC中,∠B=30°,AB=AC=4cm,点P从点A出发,以1cm/s的速度沿A→B方向勾速运动,同时点M从点B出发,以
ABC中,∠B=30°,AB=AC=4cm,点P从点A出发,以1cm/s的速度沿A→B方向勾速运动,同时点M从点B出发,以![]() cm/s的速度沿B→C方向匀速运动,当其中一个点运动至终点时,另一个点随之停止运动,连接PM,在PM右侧作∠PMG=30°,该角的另一边交射线CA于点G,连接PC.设运动时间为t(s),当△APG为等腰三角形时,直接写出t的值.
cm/s的速度沿B→C方向匀速运动,当其中一个点运动至终点时,另一个点随之停止运动,连接PM,在PM右侧作∠PMG=30°,该角的另一边交射线CA于点G,连接PC.设运动时间为t(s),当△APG为等腰三角形时,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
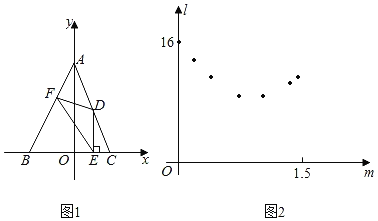
【题目】如图1,在平面直角坐标系中,△ABC的顶点A,C分別是直线y=﹣![]() x+4与坐标轴的交点,点B的坐标为(﹣2,0),点D是边AC上的一点,DE⊥BC于点E,点F在边AB上,且D,F两点关于y轴上的某点成中心对称,连结DF,EF.设点D的横坐标为m,EF2为l,请探究:
x+4与坐标轴的交点,点B的坐标为(﹣2,0),点D是边AC上的一点,DE⊥BC于点E,点F在边AB上,且D,F两点关于y轴上的某点成中心对称,连结DF,EF.设点D的横坐标为m,EF2为l,请探究:
①线段EF长度是否有最小值.
②△BEF能否成为直角三角形.
小明尝试用“观察﹣猜想﹣验证﹣应用”的方法进行探究,请你一起来解决问题.
(1)小明利用“几何画板”软件进行观察,测量,得到l随m变化的一组对应值,并在平面直角坐标系中以各对应值为坐标描点(如图2).请你在图2中连线,观察图象特征并猜想l与m可能满足的函数类别.
(2)小明结合图1,发现应用三角形和函数知识能验证(1)中的猜想,请你求出l关于m的函数表达式及自变量的取值范围,并求出线段EF长度的最小值.
(3)小明通过观察,推理,发现△BEF能成为直角三角形,请你求出当△BEF为直角三角形时m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校体育社团活动计划开设“足球、篮球、排球、乒乓球”四个体育兴趣小组,每个学生只能选报一项参加活动,为了解该社团成员选择兴趣小组的情况,某调查小组在社团中进行了一次抽样调查,绘制了如下尚不完整的统计图表.
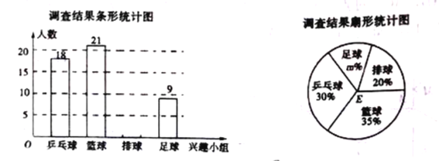
根据以上信息解答下列问题:
(1)本次抽样调查的样本容量为 ,扇形统计图中的值为 .
(2)补全条形统计图;
(3)若该学校有学生![]() 人,有
人,有![]() 的学生选择了参加体育社团活动,请你估计该校选择排球和足球这两个兴趣小组的学生大约共有多少人?
的学生选择了参加体育社团活动,请你估计该校选择排球和足球这两个兴趣小组的学生大约共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数![]() 和
和![]() 在第一象限内的图象如图所示,点P是
在第一象限内的图象如图所示,点P是![]() 的图象上一动点,作PC⊥x轴于点C,交
的图象上一动点,作PC⊥x轴于点C,交![]() 的图象于点A,作PD⊥y轴于点D,交
的图象于点A,作PD⊥y轴于点D,交![]() 的图象于点B,给出如下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积大小不会发生变化;④PA=3AC,其中正确的结论序号是( )
的图象于点B,给出如下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积大小不会发生变化;④PA=3AC,其中正确的结论序号是( )

A.①③B.②③④C.①③④D.①④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明大学毕业回家乡创业,第一期培植盆景与花卉各50盆售后统计,盆景的平均每盆利润是160元,花卉的平均每盆利润是19元,调研发现:
①盆景每增加1盆,盆景的平均每盆利润减少2元;每减少1盆,盆景的平均每盆利润增加2元;②花卉的平均每盆利润始终不变.
小明计划第二期培植盆景与花卉共100盆,设培植的盆景比第一期增加x盆,第二期盆景与花卉售完后的利润分别为W1,W2(单位:元)
(1)用含x的代数式分别表示W1,W2;
(2)当x取何值时,第二期培植的盆景与花卉售完后获得的总利润W最大,最大总利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C是圆上一点,点D是半圆的中点,连接CD交OB于点E,点F是AB延长线上一点,CF=EF.
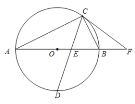
(1)求证:FC是⊙O的切线;
(2)若CF=5,![]() ,求⊙O半径的长.
,求⊙O半径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是某浴室花洒实景图,图2是该花洒的侧面示意图.已知活动调节点B可以上下调整高度,离地面CD的距离BC=160cm.设花洒臂与墙面的夹角为α,可以扭动花洒臂调整角度,且花洒臂长AB=30cm.假设水柱AE垂直AB直线喷射,小华在离墙面距离CD=120cm处淋浴.

(1)当α=30°时,水柱正好落在小华的头顶上,求小华的身高DE.
(2)如果小华要洗脚,需要调整水柱AE,使点E与点D重合,调整的方式有两种:
①其他条件不变,只要把活动调节点B向下移动即可,移动的距离BF与小华的身高DE有什么数量关系?直接写出你的结论;
②活动调节点B不动,只要调整α的大小,在图3中,试求α的度数.
(参考数据:![]() ≈1.73,sin8.6°≈0.15,sin36.9°≈0.60,tan36.9°≈0.75)
≈1.73,sin8.6°≈0.15,sin36.9°≈0.60,tan36.9°≈0.75)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com