
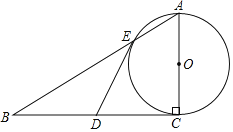
【题目】如图,AB是⊙O的直径,点C是圆上一点,点D是半圆的中点,连接CD交OB于点E,点F是AB延长线上一点,CF=EF.
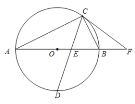
(1)求证:FC是⊙O的切线;
(2)若CF=5,![]() ,求⊙O半径的长.
,求⊙O半径的长.
【答案】(1)证明见解析;(2)AO=![]() .
.
【解析】
(1)连接OD,利用点D是半圆的中点得出∠AOD与∠BOD是直角,之后通过等量代换进一步得出∠FCE+∠OCD=∠OED+∠ODC=90°从而证明结论即可;
(2)通过![]() 得出
得出![]() =
=![]() ,再证明△ACF∽△CBF从而得出AF=10,之后进一步求解即可.
,再证明△ACF∽△CBF从而得出AF=10,之后进一步求解即可.
证明:连接OD,
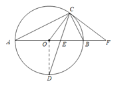
∵点D是半圆的中点,
∴∠AOD=∠BOD=90°.
∴∠ODC+∠OED=90°.
∵OD=OC,
∴∠ODC=∠OCD.
又∵CF=EF,
∴∠FCE=∠FEC.
∵∠FEC=∠OED,
∴∠FCE=∠OED.
∴∠FCE+∠OCD=∠OED+∠ODC=90°.
即FC⊥OC.
∴FC是⊙O的切线.
(2)∵tanA=![]() ,
,
∴在Rt△ABC中,![]() =
=![]() .
.
∵∠ACB=∠OCF=90°,
∴∠ACO=∠BCF=∠A.
∴△ACF∽△CBF,
∴![]() =
=![]() =
=![]() =
=![]() .
.
∴AF=10.
∴CF2=BF·AF.
∴BF=![]() .
.
∴AO=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.

(1)求证:△AEC≌△ADB;(2)若AB=2,∠BAC=45°,当四边形ADFC是菱形时,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 是直线
是直线![]() 与反比例函数
与反比例函数![]() (
(![]() 为常数)的图象的交点.过点
为常数)的图象的交点.过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,且
,且![]() .
.
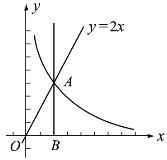
(1)求点![]() 的坐标及
的坐标及![]() 的值;
的值;
(2)已知点![]() ,过点
,过点![]() 作平行于
作平行于![]() 轴的直线,交直线
轴的直线,交直线![]() 于点
于点![]() ,交反比例函数
,交反比例函数![]() (
(![]() 为常数)的图象于点
为常数)的图象于点![]() ,交垂线
,交垂线![]() 于点
于点![]() .若
.若![]() ,结合函数的图象,直接写出
,结合函数的图象,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列对于随机事件的概率的描述:
①抛掷一枚均匀的硬币,因为“正面朝上”的概率是0.5,所以抛掷该硬币100次时,就会有50次“正面朝上”;
②一个不透明的袋子里装有4个黑球,1个白球,这些球除了颜色外无其他差别.从中随机摸出一个球,恰好是白球的概率是0.2;
③测试某射击运动员在同一条件下的成绩,随着射击次数的增加,“射中9环以上”的频率总是在0.85附近摆动,显示出一定的稳定性,可以估计该运动员“射中9环以上”的概率是0.85
其中合理的有______(只填写序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小宇设计了一个随机碰撞模拟器:在模拟器中有![]() ,
,![]() ,
,![]() 三种型号的小球,它们随机运动,当两个小球相遇时会发生碰撞(不考虑多个小球相撞的情况).若相同型号的两个小球发生碰撞,会变成一个
三种型号的小球,它们随机运动,当两个小球相遇时会发生碰撞(不考虑多个小球相撞的情况).若相同型号的两个小球发生碰撞,会变成一个![]() 型小球;若不同型号的两个小球发生碰撞,则会变成另外一种型号的小球,例如,一个
型小球;若不同型号的两个小球发生碰撞,则会变成另外一种型号的小球,例如,一个![]() 型小球和一个
型小球和一个![]() 型小球发生碰撞,会变成一个
型小球发生碰撞,会变成一个![]() 型小球.现在模拟器中有
型小球.现在模拟器中有![]() 型小球12个,
型小球12个,![]() 型小球9个,
型小球9个,![]() 型小球10个,如果经过各种两两碰撞后,最后只剩一个小球.以下说法:
型小球10个,如果经过各种两两碰撞后,最后只剩一个小球.以下说法:
①最后剩下的小球可能是![]() 型小球;
型小球;
②最后剩下的小球一定是![]() 型小球;
型小球;
③最后剩下的小球一定不是![]() 型小球.
型小球.
其中正确的说法是:( )
A.①B.②③C.③D.①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线M:y=-x2+2bx+c与直线l:y=9x+14交于点A,其中点A的横坐标为-2.
(1)请用含有b的代数式表示c: ;
(2)若点B在直线l上,且B的横坐标为-1,点C的坐标为(b,5).
①若抛物线M还过点B,直接写出该抛物线的解析式;
②若抛物线M与线段BC恰有一个交点,结合函数图象,直接写出b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知Rt△ABC,∠C=90°,D为BC的中点,以AC为直径的⊙O交AB于点E.
(1)求证:DE是⊙O的切线;
(2)若AE:EB=1:2,BC=12,求AE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com