
【题目】在平面直角坐标系xOy中,抛物线M:y=-x2+2bx+c与直线l:y=9x+14交于点A,其中点A的横坐标为-2.
(1)请用含有b的代数式表示c: ;
(2)若点B在直线l上,且B的横坐标为-1,点C的坐标为(b,5).
①若抛物线M还过点B,直接写出该抛物线的解析式;
②若抛物线M与线段BC恰有一个交点,结合函数图象,直接写出b的取值范围.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②
;②![]() 或
或![]() .
.
【解析】
(1)将A点横坐标,代入直线l:y=9x+14得到A点的坐标,再代入到抛物线中,即可求解;
(2)①将B点横坐标,代入直线l:y=9x+14得到B点的坐标,再代入到抛物线中,可求出抛物线的解析式;
②抛物线的顶点为N(![]() ),开口向下,C(b,5),B(-1,5),要使得抛物线M与线段BC有交点,N不在C的下方,即
),开口向下,C(b,5),B(-1,5),要使得抛物线M与线段BC有交点,N不在C的下方,即![]()
![]() 0,则分
0,则分![]() ,或
,或![]() 两种情况讨论,结合图象求解.
两种情况讨论,结合图象求解.
解:(1)∵抛物线M:y=-x2+2bx+c与直线l:y=9x+14交于点A,其中点A的横坐标为-2,
∴A(-2,-4),
代入y=-x2+2bx+c得![]() ,
,
∴![]() .
.
故答案为:![]() .
.
(2)∵点B在直线l:y=9x+14上,且B的横坐标为-1,
∴B(-1,5),
①若抛物线M:y=-x2+2bx+4b还过点B(-1,5),
∴![]() ,
,
∴b=3,
∴该抛物线的解析式:![]() ;
;
②∵![]() 的顶点为N(
的顶点为N(![]() ),开口向下,
),开口向下,
其中C(b,5),B(-1,5),
要使得抛物线M与线段BC有交点,N不在C的下方,即![]() 0,
0,
∴![]() ,或
,或![]() ,
,
当![]() 时,
时,
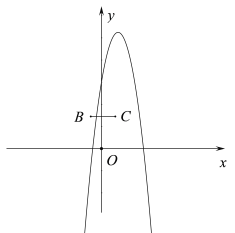
结合函数图象,若抛物线M与线段BC恰有一个交点,
当![]() 时,
时,![]() ,
,
∴![]() ;
;
当![]() 时,
时,
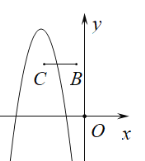
结合函数图象,若抛物线M与线段BC恰有一个交点,
当![]() 时,
时,![]() ,
,
∴![]() ;
;
综上所述:抛物线M与线段BC恰有一个交点时,![]() 或
或![]() .
.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,将函数y=![]() (x﹣2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是( )
(x﹣2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是( )

A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了解旅游人数的变化情况,收集并整理了2017年1月至2019年12月期间的月接待旅游量(单位:万人次)的数据并绘制了统计图如下:
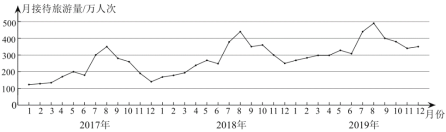
根据统计图提供的信息,下列推断不合理的是( )
A.2017年至2019年,各年的月接待旅游量高峰期大致在7,8月份
B.2019年的月接待旅游量的平均值超过300万人次
C.2017年至2019年,年接待旅游量逐年增加
D.2017年至2019年,各年下半年(7月至12月)的月接待旅游量相对于上半年(1月至6月)波动性更小,变化比较平稳
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C是圆上一点,点D是半圆的中点,连接CD交OB于点E,点F是AB延长线上一点,CF=EF.
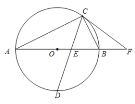
(1)求证:FC是⊙O的切线;
(2)若CF=5,![]() ,求⊙O半径的长.
,求⊙O半径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,对称轴与
两点,对称轴与![]() 轴交于点
轴交于点![]() ,点
,点![]() ,点
,点![]() ,点
,点![]() 是平面内一动点,且满足
是平面内一动点,且满足![]() 是线段
是线段![]() 的中点,连结
的中点,连结![]() .则线段
.则线段![]() 的最大值是________________.
的最大值是________________.
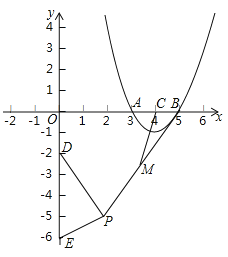
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形![]() 中,
中,![]() ,点
,点![]() 为
为![]() 边上一动点(与点
边上一动点(与点![]() 不重合),连接
不重合),连接![]() 将
将![]() 的两边所在射线
的两边所在射线![]() 以点
以点![]() 为中心,顺时针旋转
为中心,顺时针旋转![]() 分别交射线
分别交射线![]() 于点
于点![]() .
.
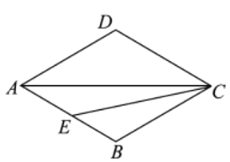
(1)依题意补全图形;
(2)若![]() ,求
,求![]() 的大小(用含
的大小(用含![]() 的式子表示) ;
的式子表示) ;
(3)用等式表示线段![]() 与
与![]() 之间的数量关系,并证明.
之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市生物和地理会考的考试结果以等级形式呈现,分A、B、C、D四个等级.某校八年级学生参加生物会考后,随机抽取部分学生的生物成绩进行统计,绘制成如下两幅不完整的统计图.
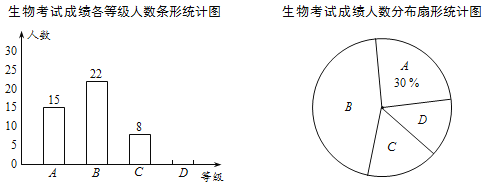
(1)这次抽样调查共抽取了 名学生的生物成绩.扇形统计图中,D等级所对应的扇形圆心角度数为 °;
(2)将条形统计图补充完整;
(3)若该校八年级有400名学生,估计这次考试有多少名学生的生物成绩等级为D级?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com