
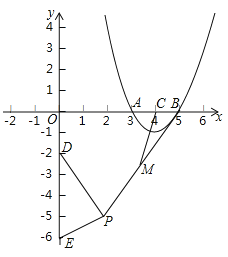
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,对称轴与
两点,对称轴与![]() 轴交于点
轴交于点![]() ,点
,点![]() ,点
,点![]() ,点
,点![]() 是平面内一动点,且满足
是平面内一动点,且满足![]() 是线段
是线段![]() 的中点,连结
的中点,连结![]() .则线段
.则线段![]() 的最大值是________________.
的最大值是________________.
【答案】![]()
【解析】
首先通过解方程![]() 得出点A的坐标,然后进一步根据抛物线性质得出点C为AB的中点,结合题意,利用勾股定理求出AQ,然后根据题意得出点P在以DE为直径的圆上,圆心Q点的坐标为(
得出点A的坐标,然后进一步根据抛物线性质得出点C为AB的中点,结合题意,利用勾股定理求出AQ,然后根据题意得出点P在以DE为直径的圆上,圆心Q点的坐标为(![]() ,0),圆Q的半径为2,然后延长AQ较圆Q于点F,得出此时AF最大,再连接AP,利用三角形中位线性质进一步求解即可.
,0),圆Q的半径为2,然后延长AQ较圆Q于点F,得出此时AF最大,再连接AP,利用三角形中位线性质进一步求解即可.
解方程![]() 可得
可得![]() ,
,![]() ,
,
则:点A坐标为(3,0),点B坐标为(5,0),
∵抛物线的对称轴与![]() 轴交于点C,
轴交于点C,
∴点C为AB的中点,
设DE的中点为Q,则Q点的坐标为(![]() ,0),
,0),
∴根据勾股定理可得:AQ=![]() ,
,
∵∠DPE=90°,
∴点P在以DE为直径的圆上,圆心Q点的坐标为(![]() ,0),圆Q的半径为2,
,0),圆Q的半径为2,
如图,延长AQ较圆Q于点F,此时AF最大,最大值为![]() ,
,
再连接AP,

∵点M是线段PB中点,
∴CM为△ABP的中位线,
∴CM=![]() AP,
AP,
∴CM的最大值为:![]() ,
,
故答案为:![]() .
.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:
【题目】为了解学生在假期中的课外阅读情况,七(1)班针对“你最喜爱的课外阅读书目“进行调查(每名学生必须选一类且只能选一类阅读书目),并根据调查结果列出统计表,绘制成扇形统计图.
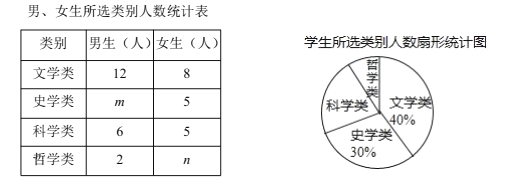
(1)m=__________,n=__________;
(2)扇形统计图中“科学类”所对应扇形圆心角度数为__________°;
(3)从选哲学类的学生中,随机选取两名学生参加学校团委组织的辩论赛,请用树状图或列表法求出所选取的两名学生都是男生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 是直线
是直线![]() 与反比例函数
与反比例函数![]() (
(![]() 为常数)的图象的交点.过点
为常数)的图象的交点.过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,且
,且![]() .
.
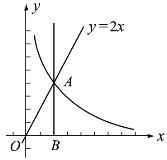
(1)求点![]() 的坐标及
的坐标及![]() 的值;
的值;
(2)已知点![]() ,过点
,过点![]() 作平行于
作平行于![]() 轴的直线,交直线
轴的直线,交直线![]() 于点
于点![]() ,交反比例函数
,交反比例函数![]() (
(![]() 为常数)的图象于点
为常数)的图象于点![]() ,交垂线
,交垂线![]() 于点
于点![]() .若
.若![]() ,结合函数的图象,直接写出
,结合函数的图象,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小宇设计了一个随机碰撞模拟器:在模拟器中有![]() ,
,![]() ,
,![]() 三种型号的小球,它们随机运动,当两个小球相遇时会发生碰撞(不考虑多个小球相撞的情况).若相同型号的两个小球发生碰撞,会变成一个
三种型号的小球,它们随机运动,当两个小球相遇时会发生碰撞(不考虑多个小球相撞的情况).若相同型号的两个小球发生碰撞,会变成一个![]() 型小球;若不同型号的两个小球发生碰撞,则会变成另外一种型号的小球,例如,一个
型小球;若不同型号的两个小球发生碰撞,则会变成另外一种型号的小球,例如,一个![]() 型小球和一个
型小球和一个![]() 型小球发生碰撞,会变成一个
型小球发生碰撞,会变成一个![]() 型小球.现在模拟器中有
型小球.现在模拟器中有![]() 型小球12个,
型小球12个,![]() 型小球9个,
型小球9个,![]() 型小球10个,如果经过各种两两碰撞后,最后只剩一个小球.以下说法:
型小球10个,如果经过各种两两碰撞后,最后只剩一个小球.以下说法:
①最后剩下的小球可能是![]() 型小球;
型小球;
②最后剩下的小球一定是![]() 型小球;
型小球;
③最后剩下的小球一定不是![]() 型小球.
型小球.
其中正确的说法是:( )
A.①B.②③C.③D.①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线M:y=-x2+2bx+c与直线l:y=9x+14交于点A,其中点A的横坐标为-2.
(1)请用含有b的代数式表示c: ;
(2)若点B在直线l上,且B的横坐标为-1,点C的坐标为(b,5).
①若抛物线M还过点B,直接写出该抛物线的解析式;
②若抛物线M与线段BC恰有一个交点,结合函数图象,直接写出b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
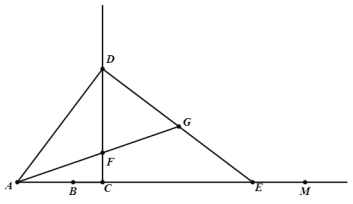
【题目】如图,射线AM上有一点B,AB=6.点C是射线AM上异于B的一点,过C作CD⊥AM,且CD=![]() AC.过D点作DE⊥AD,交射线AM于E. 在射线CD取点F,使得CF=CB,连接AF并延长,交DE于点G.设AC=3x.
AC.过D点作DE⊥AD,交射线AM于E. 在射线CD取点F,使得CF=CB,连接AF并延长,交DE于点G.设AC=3x.
(1) 当C在B点右侧时,求AD、DF的长.(用关于x的代数式表示)
(2)当x为何值时,△AFD是等腰三角形.
(3)若将△DFG沿FG翻折,恰使点D对应点![]() 落在射线AM上,连接
落在射线AM上,连接![]() ,
,![]() .此时x的值为 (直接写出答案)
.此时x的值为 (直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现如图1,在![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,![]() ,连接
,连接![]() 交于点
交于点![]() .填空:①
.填空:①![]() 的值为______;②
的值为______;②![]() 的度数为______.
的度数为______.
(2)类比探究如图2,在![]() 和
和![]() 中,
中,![]() ,
,![]() ,连接
,连接![]() 交
交![]() 的延长线于点
的延长线于点![]() .请判断
.请判断![]() 的值及
的值及![]() 的度数,并说明理由;
的度数,并说明理由;
(3)拓展延伸在(2)的条件下,将![]() 绕点
绕点![]() 在平面内旋转,
在平面内旋转,![]() 所在直线交于点
所在直线交于点![]() ,若
,若![]() ,
,![]() ,请直接写出当点
,请直接写出当点![]() 与点
与点![]() 在同一条直线上时
在同一条直线上时![]() 的长.
的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com