
【题目】如图,在![]() 中,
中,![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 与边
与边![]() 相切于点
相切于点![]() ,交
,交![]() 于点
于点![]() 为
为![]() 的直径.
的直径.
(1)求证:![]() ;
;
(2)若![]() ,求
,求![]() 的长.
的长.
【答案】(1)证明见解析;(2)![]()
【解析】
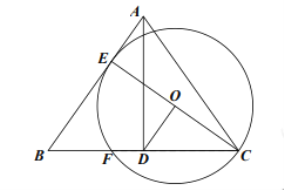
(1)根据圆的切线的性质得出CE⊥AB,然后进一步利用AB=AC和AD⊥BC证明得BD=DC,从而根据三角形中位线性质得知OD∥EB,由此即可证明结论;
(2)连接EF,首先根据题意得出∠BEF+∠FEC=∠FEC+∠ECF=90°,由此求出∠ECF=∠BEF,再者利用三角函数得出![]() ,从而求出EF,再利用勾股定理求得BE,最后利用平行线分线段成比例的性质进一步求解即可.
,从而求出EF,再利用勾股定理求得BE,最后利用平行线分线段成比例的性质进一步求解即可.
(1)∵![]() 与边AB相切于点E,且CE为
与边AB相切于点E,且CE为![]() 的直径,
的直径,
∴CE⊥AB,OE=OC,
∵AB=AC,AD⊥BC,
∴BD=DC,
又∵OE=OC,
∴OD是△BCE的中位线,
∴OD∥EB,
∴OD⊥CE;
(2)如图,连接EF,

∵CE为![]() 的直径,且点F在
的直径,且点F在![]() 上,
上,
∴∠EFC=90°,
∵CE⊥AB,
∴∠BEC=90°,
∴∠BEF+∠FEC=∠FEC+∠ECF=90°,
∴∠ECF=∠BEF,
∴tan∠BEF=tan∠ECF,
∴![]() ,
,
又∵DF=1,BD=DC=3,
∴BF=2,FC=4,
∴![]() ,
,
∴EF=![]() ,
,
∵∠EFC=90°,
∴∠BFE=90°,
由勾股定理可得:BE=![]() ,
,
∵AD⊥BC且∠EFC=90°,
∴EF∥AD,
∴![]() ,
,
∴AE=![]() .
.


科目:初中数学 来源: 题型:
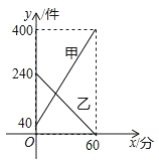
【题目】某快递公司每天上午9:00-10:00为集中揽件和派件时段,甲仓库用来揽收快件,乙仓库用来派发快件,该时段内甲、乙两仓库的快件数量y(件)与时间x(分)之间的函数图象如图所示,那么当两仓库快递件数相同时,此刻的时间为__________;
查看答案和解析>>
科目:初中数学 来源: 题型:
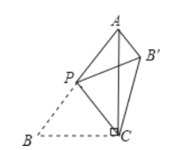
【题目】如图,在△ABC中,∠ACB=90°,AB=5,BC=3,P是AB边上的动点(不与点B重合)将△BCP沿CP所在的直线翻折,得到![]() ,连接
,连接![]() ,下面有四个判断:
,下面有四个判断:
①当AP=BP时,![]() ∥CP;
∥CP;
②当AP=BP时,![]()
③当CP⊥AB时,![]() ;
;
④![]() 长度的最小值是1.
长度的最小值是1.
所有正确结论的序号是( )
A.①③④B.①②C.①②④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种型号的电热水器工作过程如下:在接通电源以后,从初始温度20![]() 下加热水箱中的水,当水温达到设定温度60
下加热水箱中的水,当水温达到设定温度60![]() 时,加热停止;此后水箱中的水温开始逐渐下降,当下降到保温温度30
时,加热停止;此后水箱中的水温开始逐渐下降,当下降到保温温度30![]() 时,再次自动加热水箱中的水至60
时,再次自动加热水箱中的水至60![]() ,加热停止;当水箱中的水温下降到30
,加热停止;当水箱中的水温下降到30![]() 时,再次自动加热,……,按照以上方式不断循环.小宇根据学习函数的经验,对该型号电热水器水箱中的水温随时间变化的规律进行了探究,发现水温
时,再次自动加热,……,按照以上方式不断循环.小宇根据学习函数的经验,对该型号电热水器水箱中的水温随时间变化的规律进行了探究,发现水温![]() 是时间
是时间![]() 的函数,其中
的函数,其中![]() (单位:
(单位:![]() )表示水箱中水的温度,
)表示水箱中水的温度,![]() (单位:
(单位:![]() )表示接通电源后的时间.下面是小宇的探究过程,请补充完整:
)表示接通电源后的时间.下面是小宇的探究过程,请补充完整:
(1)小宇记录了从初始温度20![]() 第一次加热至设定温度60
第一次加热至设定温度60![]() ,之后水温冷却至保温温度30
,之后水温冷却至保温温度30![]() 的过程中,
的过程中,![]() 随
随![]() 的变化情况,如下表所示:
的变化情况,如下表所示:
接通电源后的时间 | 0 | 2 | 4 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | … |
水箱中水的温度 | 20 | 30 | 40 | 60 | 51 | 45 | 40 | 36 | 33 | 30 |
①请写出一个符合加热阶段![]() 与
与![]() 关系的函数解析式______________;
关系的函数解析式______________;
②根据该电热水器的工作特点,当第二次加热至设定温度60![]() 时,距离接通电源的时间
时,距离接通电源的时间![]() 为________
为________![]() .
.
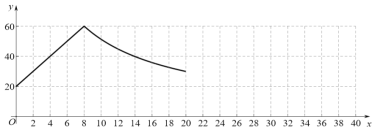
(2)根据上述的表格,小宇画出了当![]() 时的函数图象,请根据该电热水器的工作特点,帮他画出当
时的函数图象,请根据该电热水器的工作特点,帮他画出当![]() 时的函数图象.
时的函数图象.
(3)已知适宜人体沐浴的水温约为![]() ,小宇在上午8点整接通电源,水箱中水温为20
,小宇在上午8点整接通电源,水箱中水温为20![]() ,热水器开始按上述模式工作,若不考虑其他因素的影响,请问在上午9点30分时,热水器的水温______(填“是”或“否”)适合他沐浴,理由是_________________.
,热水器开始按上述模式工作,若不考虑其他因素的影响,请问在上午9点30分时,热水器的水温______(填“是”或“否”)适合他沐浴,理由是_________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
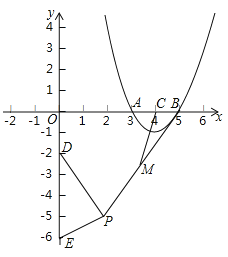
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,对称轴与
两点,对称轴与![]() 轴交于点
轴交于点![]() ,点
,点![]() ,点
,点![]() ,点
,点![]() 是平面内一动点,且满足
是平面内一动点,且满足![]() 是线段
是线段![]() 的中点,连结
的中点,连结![]() .则线段
.则线段![]() 的最大值是________________.
的最大值是________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明对函数 的图象和性质进行了探究.已知当自变量
的图象和性质进行了探究.已知当自变量![]() 的值为1时,函数值为4;当自变量
的值为1时,函数值为4;当自变量![]() 的值为2时,函数值为3;探究过程如下,请补充完整:
的值为2时,函数值为3;探究过程如下,请补充完整:
(1)求这个函数的表达式;
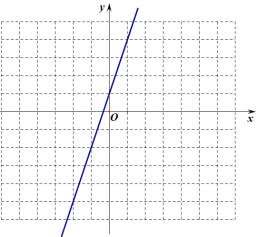
(2)在给出的平面直角坐标系中,画出这个函数的图象并写出这个函数的一条性质: ;
(3)进一步探究函数图象并解决问题:已知函数![]() 的图象如图所示,结合你所画的函数图象,写出不等式
的图象如图所示,结合你所画的函数图象,写出不等式![]() 的解集: .
的解集: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,平行四边形ABCD中,AB⊥AC,AB=6,AD=10,点P在边AD上运动,以P为圆心,PA为半径的⊙P与对角线AC交于A,E两点.不难发现,随着AP的变化,⊙P与平行四边形ABCD的边的公共点的个数也在变化.如图2,当⊙P与边CD相切时,⊙P与平行四边形ABCD的边有三个公共点.若公共点的个数为4,则相对应的AP的取值范围为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
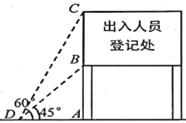
【题目】2020年春节期间,昆明市政府为了进一步做好新冠肺炎疫情的防控工作,在各个高速公路出入口均设立检测点,对出入人员进行登记和体温检测,下图为一高速路口检测点的指示牌,已知立杆![]() 的高度是
的高度是![]() ,从侧面
,从侧面![]() 点处测得指示牌
点处测得指示牌![]() 点和
点和![]() 点的仰角分别是
点的仰角分别是![]() 和
和![]() ,求
,求![]() 的长.(结果精确到
的长.(结果精确到![]() .参考数据:
.参考数据:![]() ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com