练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

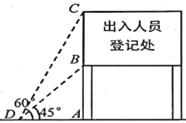
    【题目】2020年春节期间，昆明市政府为了进一步做好新冠肺炎疫情的防控工作，在各个高速公路出入口均设立检测点，对出入人员进行登记和体温检测，下图为一高速路口检测点的指示牌，已知立杆的高度是，从侧面点处测得指示牌点和点的仰角分别是和，求的长．（结果精确到．参考数据：，）

    【答案】2.2m

    【解析】

    在Rt△ABD中，由∠BDA=45°，AB=3，可得出AD=3，在Rt△ACD中，由特殊角的正切值即可得出线段AC的长度，再利用线段间的关系即可得出结论．

    解：在Rt△ABD中，∵∠BDA=45°，AB=3

    ∴AD=3

    在Rt△ACD中，∵∠ADC=60°

    ∴tan60°=

    ∴AC= tan60°·AD=·3=3

    ∴BC=AC-AB=3-32.2m

    故答案为：2.2m

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在中，于点，过点作与边相切于点，交于点为的直径．

    （1）求证：；

    （2）若，求的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在△ABC中，∠BAC=90°，AB=2AC，点A（2，0）、B（0，4），点C在第一象限内，双曲线y=（x＞0）经过点C．将△ABC沿y轴向上平移m个单位长度，使点A恰好落在双曲线上，则m的值为________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在一个不透明的布袋中装有标着数字2，3，4，5的4个小球，这4个小球的材质、大小和形状完全相同，现从中随机摸出两个小球，这两个小球上的数字之积大于9的概率为(　　)

    A.B.C.D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）问题发现如图1，在和中，，，，连接交于点.填空：①的值为______；②的度数为______．

    （2）类比探究如图2，在和中，，，连接交的延长线于点.请判断的值及的度数，并说明理由；

    （3）拓展延伸在（2）的条件下，将绕点在平面内旋转，所在直线交于点，若，，请直接写出当点与点在同一条直线上时的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】甲、乙、丙、丁两位同学做传球游戏：第一次由甲将球随机传给乙、丙、丁中的某一人，从第二次起，每一次都由持球者将球再随机传给其他三人中的某一人，则第二次传球后球回到甲手里的概率是________；第三次传球后球回到甲手里的概率是________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

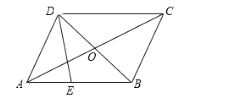
    【题目】如图，在平行四边形ABCD中，对角线AC、BD相交于点O．E为边AB上一点，且BE = 2AE．设，．

    （1）填空：向量 ；

    （2）如果点F是线段OC的中点，那么向量 ，并在图中画出向量在向量和方向上的分向量．

    注：本题结果用向量的式子表示．画图不要求写作法，但要指出所作图中表示结论的向量．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某市居民用水实行以户为单位的三级阶梯收费办法：

    第一级：居民每户每月用水吨以内含吨，每吨收水费元；

    第二级：居民每户每月用水超过吨但不超过吨，未超过的部分按照第一级标准收费，超过部分每吨收水费元；

    第三级：居民每户每月用水超过吨，未超过吨的部分按照第一、二级标准收费，超过部分每吨收水费元；

    设一户居民月用水吨，应缴水费元，与之间的函数关系如图所示，

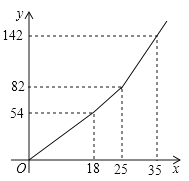
    （Ⅰ）根据图象直接作答：___________，_______________，_______________；

    （Ⅱ）求当时，与之间的函数关系式；

    （Ⅲ）把上述水费阶梯收费办法称为方案①，假设还存在方案②；居民每户月用水一律按照每吨元的标准缴费.当居民用户月用水超过吨时，请你根据居民每户月用水量的大小设计出对居民缴费最实惠的方案.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校调查了若干名家长对“初中生带手机上学”现象的看法，统计整理并制作了如下的条形与扇形统计图，根据图中提供的信息，完成以下问题：

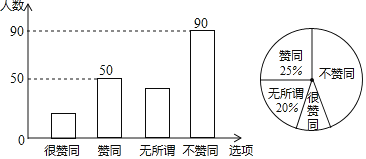
    （1）本次共调查了　 　名家长；扇形统计图中“很赞同”所对应的圆心角是　 　度．已知该校共有1600名家长，则“不赞同”的家长约有　 　名；请补全条形统计图；

    （2）从“不赞同”的五位家长中（两女三男），随机选取两位家长对全校家长进行“学生使用手机危害性”的专题讲座，请用树状图或列表法求出选中“1男1女”的概率．

    查看答案和解析>>

    同步练习册答案