
����Ŀ��ij�о�����ˮʵ���Ի�Ϊ��λ�����������շѰ취��
��һ��������ÿ��ÿ����ˮ![]() �����ں�
�����ں�![]() �֣�ÿ����ˮ��
�֣�ÿ����ˮ��![]() Ԫ��
Ԫ��
�ڶ���������ÿ��ÿ����ˮ����![]() �ֵ�������
�ֵ�������![]() �֣�δ����
�֣�δ����![]() �IJ��ְ��յ�һ�����շѣ���������ÿ����ˮ��
�IJ��ְ��յ�һ�����շѣ���������ÿ����ˮ��![]() Ԫ��
Ԫ��
������������ÿ��ÿ����ˮ����![]() �֣�δ����
�֣�δ����![]() �ֵIJ��ְ��յ�һ���������շѣ���������ÿ����ˮ��
�ֵIJ��ְ��յ�һ���������շѣ���������ÿ����ˮ��![]() Ԫ��
Ԫ��
��һ����������ˮ![]() �֣�Ӧ��ˮ��
�֣�Ӧ��ˮ��![]() Ԫ��
Ԫ��![]() ��
��![]() ֮��ĺ�����ϵ��ͼ��ʾ��
֮��ĺ�����ϵ��ͼ��ʾ��
������ͼ��ֱ������![]() ___________��
___________��![]() _______________��
_______________��![]() _______________��
_______________��
������![]() ʱ��
ʱ��![]() ��
��![]() ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
��������ˮ�ѽ����շѰ취��Ϊ�����٣����軹���ڷ����ڣ�����ÿ������ˮһ�ɰ���ÿ��![]() Ԫ�ı��ɷ�.�������û�����ˮ����
Ԫ�ı��ɷ�.�������û�����ˮ����![]() ��ʱ��������ݾ���ÿ������ˮ���Ĵ�С��Ƴ��Ծ���ɷ���ʵ�ݵķ���.
��ʱ��������ݾ���ÿ������ˮ���Ĵ�С��Ƴ��Ծ���ɷ���ʵ�ݵķ���.
���𰸡�����![]() ������
������![]() ������
������![]() ʱ��ѡ��ɷѷ����ٸ�ʵ�ݣ���
ʱ��ѡ��ɷѷ����ٸ�ʵ�ݣ���![]() ʱ��ѡ�����ֽɷѷ���������ͬ����
ʱ��ѡ�����ֽɷѷ���������ͬ����![]() ʱ��ѡ��ɷѷ����ڸ�ʵ��.
ʱ��ѡ��ɷѷ����ڸ�ʵ��.
��������
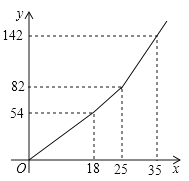
��1�����ݵ���=�ܼ����������������a��b��c��ֵ��
��2���۲캯��ͼ���ҳ�������꣬���ô���ϵ�������������x��25ʱy��x֮��ĺ�����ϵ��
��3�����ܼ�=�������������ҳ�ѡ��ɷѷ������轻ˮ��y��Ԫ������ˮ����x���֣�֮��ĺ�����ϵʽ���ֱ��ҳ���6x-68��4x��6x-68=4x��6x-68��4xʱx��ȡֵ��Χ��x��ֵ����ѡ����õ͵ķ������ɵó����ۣ�
�⣺����a=54��18=3��
b=��82-54������25-18��=4��
c=��142-82������35-25��=6��
�ʴ�Ϊ��3,��4��6��
�����赱x��25ʱ��y��x֮��ĺ�����ϵʽΪy=mx+n��m��0����
����25��82������35��142������y=mx+n���ã�![]() ��
��
��ã�![]() ��
��
�൱![]() ʱ��
ʱ��![]() ��
��![]() ֮��ĺ�����ϵʽΪ
֮��ĺ�����ϵʽΪ![]() .
.
����ѡ��ɷѷ������轻ˮ��![]() ��Ԫ������ˮ��
��Ԫ������ˮ��![]() ���֣�֮��ĺ�����ϵʽΪ
���֣�֮��ĺ�����ϵʽΪ![]() .
.
��![]() ʱ��
ʱ��![]() ��
��
��![]() ʱ��
ʱ��![]() ��
��
��![]() ��
��![]() .
.
�൱![]() ʱ��ѡ��ɷѷ����ٸ�ʵ�ݣ���
ʱ��ѡ��ɷѷ����ٸ�ʵ�ݣ���![]() ʱ��ѡ�����ֽɷѷ���������ͬ����
ʱ��ѡ�����ֽɷѷ���������ͬ����![]() ʱ��ѡ��ɷѷ����ڸ�ʵ��.
ʱ��ѡ��ɷѷ����ڸ�ʵ��.


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��ƽ���ı���ABCD�У�AB��AC��AB��6��AD��10����P�ڱ�AD���˶�����PΪԲ�ģ�PAΪ�뾶����P��Խ���AC����A��E���㣮���ѷ��֣�����AP�ı仯����P��ƽ���ı���ABCD�ıߵĹ�����ĸ���Ҳ�ڱ仯����ͼ2������P���CD����ʱ����P��ƽ���ı���ABCD�ı������������㣮��������ĸ���Ϊ4�������Ӧ��AP��ȡֵ��ΧΪ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
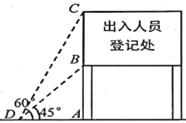
����Ŀ��2020�괺���ڼ䣬����������Ϊ�˽�һ�������¹ڷ�������ķ��ع������ڸ������ٹ�·����ھ��������㣬�Գ�����Ա���еǼǺ����¼�⣬��ͼΪһ����·�ڼ����ָʾ�ƣ���֪����![]() �ĸ߶���
�ĸ߶���![]() ���Ӳ���
���Ӳ���![]() �㴦���ָʾ��
�㴦���ָʾ��![]() ���
���![]() ������Ƿֱ���
������Ƿֱ���![]() ��
��![]() ����
����![]() �ij����������ȷ��
�ij����������ȷ��![]() ���ο����ݣ�
���ο����ݣ�![]() ��
��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
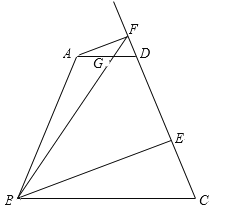
����Ŀ����ͼ��������ABCD�У�AD // BC��AB = CD��AD = 5��BC = 15��![]() ��EΪ����CD������һ�㣬����A��AF // BE��������CD�ཻ�ڵ�F������BF����ֱ��AD�ཻ�ڵ�G����CE = x��
��EΪ����CD������һ�㣬����A��AF // BE��������CD�ཻ�ڵ�F������BF����ֱ��AD�ཻ�ڵ�G����CE = x��![]() ��
��
��1����AB�ij���
��2������G���߶�AD��ʱ����y����x�ĺ�������ʽ����д�������Ķ�����
��3�����![]() �����߶�CE�ij���
�����߶�CE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
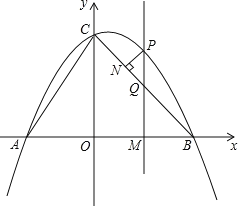
����Ŀ����ͼ��������![]() ��
��![]() ����
����![]() ���㣬��
���㣬��![]() �ύ�ڵ�
�ύ�ڵ�![]() ������
������![]() ����
����![]() �ǵ�һ�������������ϵ�һ�����㣬��
�ǵ�һ�������������ϵ�һ�����㣬��![]() �ĺ�����Ϊ
�ĺ�����Ϊ![]() ��
��
(1)��������ߵı���ʽ��
(2)����![]() ��
��![]() �ᣬ����Ϊ��
�ᣬ����Ϊ��![]() ��
��![]() ��
��![]() �ڵ�
�ڵ�![]() ����̽����P���˶������У��Ƿ���������ĵ�
����̽����P���˶������У��Ƿ���������ĵ�![]() ��ʹ����
��ʹ����![]() Ϊ������������ǵ��������Σ������ڣ��������ʱ��
Ϊ������������ǵ��������Σ������ڣ��������ʱ��![]() �����꣬�������ڣ���˵�����ɣ�
�����꣬�������ڣ���˵�����ɣ�
(3)����![]() ��
��![]() ��������
������Ϊ��![]() �����ú�
�����ú�![]() �Ĵ���ʽ��ʾ�߶�
�Ĵ���ʽ��ʾ�߶�![]() �ij����������
�ij����������![]() Ϊ��ֵʱ
Ϊ��ֵʱ![]() �����ֵ�����ֵ�Ƕ��٣�
�����ֵ�����ֵ�Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѧУ�˶����������Զ��1���������������������ֳ�Ԥ���;��������Σ��±�Ϊ�μ������������10��ѧ����Ԥ���ɼ���
ѧ����� �ɼ� ��Ŀ | 3104 | 3508 | 3115 | 3406 | 3317 | 3413 | 3218 | 3307 | 3519 | 3210 |
������Զ����λ���ף� | 1.96 | 1.92 | 1.82 | 1.80 | 1.78 | 1.76 | 1.74 | 1.72 | 1.68 | 1.60 |
1��������������� | 163 |
| 175 | 160 | 163 | 172 | 170 |
|
| 165 |
����10��ѧ���У�ͬʱ�������������ֻ��6�ˣ�����������Զ��������8![]() ��ֵ��__________��
��ֵ��__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У�������C1��y��ax2��2ax��3a��a��0���͵�A��0����3��������A����ƽ��2����λ��������ƽ��5����λ���õ���B��
��1�����B�����ꣻ
��2����������C1�ĶԳ��
��3����������C1��x�ᷭ�ۣ��õ�һ����������C2��������C2��������C1��ɵ�ͼ���ΪG����ͼ��G���߶�ABǡ��һ������ʱ�����ͼ����a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
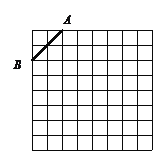
����Ŀ����ͼ�ǹ��Ϊ8��8�������������������������а�����Ҫ�������
��1�����������н���ƽ��ֱ������ϵ��ʹA������Ϊ����2��4����B������Ϊ����4��2����
��2���ڵڶ������ڵĸ�㣨�����ߵĽ��㣩�ϻ�һ��C��ʹ��C���߶�AB���һ����ABΪ�ĵ��������Σ�������������������C������͡�ABC���ܳ�������������ţ���
��3��������ABC�Ե�CΪ��ת���ģ���ת180���ġ�DEC������AE��BD����˵���ı���ABDE��ʲô�����ı��Σ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���ACB��90�㣬��ABC��30�㣬��CDE�ǵȱ������Σ���D�ڱ�AB�ϣ�

��1����ͼ1������E�ڱ�BC��ʱ����֤DE��EB��
��2����ͼ2������E�ڡ�ABC�ڲ�ʱ������ED��EB������ϵ��������֤����
��3����ͼ3������E�ڡ�ABC�ⲿʱ��EH��AB�ڵ�H������E��GE��AB�����߶�AC���ӳ����ڵ�G��AG��5CG��BH��3����CG�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com