练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】学校运动会的立定跳远和1分钟跳绳两个单项比赛分成预赛和决赛两个阶段．下表为参加这两项比赛的10名学生的预赛成绩：

    学生编号

    成绩

    项目

    3104

    3508

    3115

    3406

    3317

    3413

    3218

    3307

    3519

    3210

    立定跳远（单位：米）

    1.96

    1.92

    1.82

    1.80

    1.78

    1.76

    1.74

    1.72

    1.68

    1.60

    1分钟跳绳（单位：次）

    163

    175

    160

    163

    172

    170

    165

    在这10名学生中，同时进入两项决赛的只有6人，进入立定跳远决赛的有8人，如果知道在同时进入两项决赛的6人中有“3508号”学生，没有“3307号”学生，那么的值是__________．

    【答案】161或162或163

    【解析】

    首先确定进入立定跳远决赛的有8人，再推出1分钟跳绳的6人，构建不等式解决问题即可．

    ∵进入立定跳远决赛的有8人，
    ∴3104，3508，3115，3406，3317，3413，3218，3307的学生进入定跳远决赛，
    ∵同时进入两项决赛的只有6人，且两项决赛的6人中有“3508号”学生，没有“3307号”学生
    ∴3115，3413，3218，3104，3317进入1分钟跳绳，
    ∴＞160，＜163，

    ∴，
    ∴161或162或163．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在半径为4的⊙O中，CD为直径，AB⊥CD且过半径OD的中点，点E为⊙O上一动点，CF⊥AE于点F.当点E从点B出发顺时针运动到点D时，点F所经过的路径长为( )

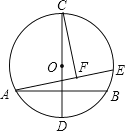
    A. B. C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

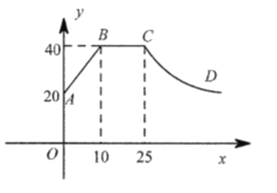
    【题目】一般情况下，学生注意力上课后逐渐增强，中间有段时间处于较理想的稳定状态，随后开始分散．实验结果表明，学生注意力指数y随时间x(min)的变化规律如图所示(其中分别为线段，为双曲线的一部分)：

    （1）上课后第与第相比较，何时学生注意力更集中？

    （2）某道难题需连续讲，为保证效果，学生注意力指数不宜低于，老师能否在所需要求下讲完这道题？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图（1），已知点G在正方形ABCD的对角线AC上，GE⊥BC，垂足为点E，GF⊥CD，垂足为点F．

    （1）证明与推断：

    ①求证：四边形CEGF是正方形；

    ②推断：的值为　 　：

    （2）探究与证明：

    将正方形CEGF绕点C顺时针方向旋转α角（0°＜α＜45°），如图（2）所示，试探究线段AG与BE之间的数量关系，并说明理由：

    （3）拓展与运用：

    正方形CEGF在旋转过程中，当B，E，F三点在一条直线上时，如图（3）所示，延长CG交AD于点H．若AG=6，GH=2，则BC=　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，的半径为，点与圆心不重合，给出如下定义：若在上存在一点，使，则称点为的特征点．

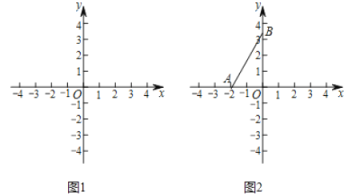
    （1）当的半径为1时，如图1．

    ①在点，，中，的特征点是__________．

    ②点在直线上，若点为的特征点，求的取值范围．

    （2）如图2，的圆心在轴上，半径为2，点，．若线段上的所有点都是的特征点，直接写出圆心的横坐标的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读理解：对于任意正实数a、b，∵≥0，　∴≥0，

    ∴≥，只有当a＝b时，等号成立．

    结论：在≥（a、b均为正实数）中，若ab为定值p，则a+b≥，只有当a＝b时，a+b有最小值．

    根据上述内容，回答下列问题：

    若m＞0，只有当m＝ 时，有最小值 ．

    思考验证：如图1，AB为半圆O的直径，C为半圆上任意一点（与点A、B不重合），过点C作CD⊥AB，垂足为D，AD＝a，DB＝b．

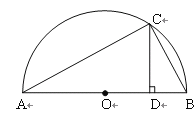
    试根据图形验证≥，并指出等号成立时的条件．

    探索应用：如图2，已知A(－3，0)，B(0，－4)，P为双曲线（x＞0）上的任意一点，过点P作PC⊥x轴于点C，PD⊥y轴于点D．求四边形ABCD面积的最小值，并说明此时四边形ABCD的形状．

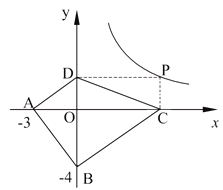
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，抛物线y＝x2+（m﹣2）x﹣2m（m＞0）与x轴交于A、B两点（A在B左边），与y轴交于点C．连接AC、BC，D为抛物线上一动点（D在B、C两点之间），OD交BC于E点．

    （1）若△ABC的面积为8，求m的值；

    （2）在（1）的条件下，求的最大值；

    （3）如图2，直线y＝kx+b与抛物线交于M、N两点（M不与A重合，M在N左边），连MA，作NH⊥x轴于H，过点H作HP∥MA交y轴于点P，PH交MN于点Q，求点Q的横坐标．

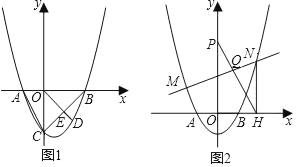
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，矩形纸片，是的中点，是上一动点，沿折叠，点落在点处；延长交于点，连接.

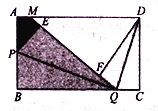
    （1）求证：≌；

    （2）当时，将沿折叠，点落在线段上点处.

    ①求证：∽；

    ②如果，，求的长.

    查看答案和解析>>

    同步练习册答案