
【题目】阅读理解:对于任意正实数a、b,∵![]() ≥0, ∴
≥0, ∴![]() ≥0,
≥0,
∴![]() ≥
≥![]() ,只有当a=b时,等号成立.
,只有当a=b时,等号成立.
结论:在![]() ≥
≥![]() (a、b均为正实数)中,若ab为定值p,则a+b≥
(a、b均为正实数)中,若ab为定值p,则a+b≥![]() ,只有当a=b时,a+b有最小值
,只有当a=b时,a+b有最小值![]() .
.
根据上述内容,回答下列问题:
若m>0,只有当m= 时,![]() 有最小值 .
有最小值 .
思考验证:如图1,AB为半圆O的直径,C为半圆上任意一点(与点A、B不重合),过点C作CD⊥AB,垂足为D,AD=a,DB=b.
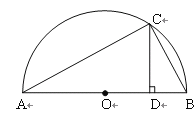
试根据图形验证![]() ≥
≥![]() ,并指出等号成立时的条件.
,并指出等号成立时的条件.
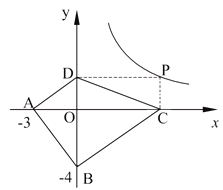
探索应用:如图2,已知A(-3,0),B(0,-4),P为双曲线![]() (x>0)上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时四边形ABCD的形状.
(x>0)上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时四边形ABCD的形状.
【答案】阅读理解:1;2;思考验证:证明见解析;当CD等于半径时,等号成立;探索应用:24;菱形.
【解析】
阅读理解:读懂题意即可得到结果;
思考验证:先证Rt△CAD∽Rt△BCD,根据相似三角形的对应边乘比例即可表示出CD,分两种情况讨论:
若点D与O不重合,连OC,在Rt△OCD中,![]() ;若点D与O重合,
;若点D与O重合,![]()
综上所述,![]() ,当CD等于半径时,等号成立.
,当CD等于半径时,等号成立.
探索应用:设出点P的坐标,即可表示出CA、DB,从而得到四边形ABCD面积的函数关系式,根据函数关系式的特征即可得到结果.
解:(1)∵a+b≥![]() (a、b均为正实数)中,若ab为定值p,则a+b≥2
(a、b均为正实数)中,若ab为定值p,则a+b≥2![]() ,只有当a=b时,a+b有最小值2
,只有当a=b时,a+b有最小值2![]() .
.
∴![]() ,
,
∴![]() ,
,
当m=![]() 时,
时,
解得:m=1或-1(不合题意舍去),
故当m=1(填![]() 不扣分),最小值是2;
不扣分),最小值是2;
故答案为:1;2;
思考验证:∵AB是的直径,
∴AC⊥BC
又∵CD⊥AB
∴∠CAD=∠BCD=90°-∠B
∴Rt△CAD∽Rt△BCD, CD2=AD·DB, ∴CD=![]()
若点D与O不重合,连OC,在Rt△OCD中,
∵OC>CD,
∴![]() ,
,
若点D与O重合时,OC=CD,∴![]()
综上所述,![]() ,即
,即![]() ,当CD等于半径时,等号成立.
,当CD等于半径时,等号成立.
探索应用:设![]() , 则
, 则![]() ,
,![]() ,
,
![]() ,化简得:
,化简得:![]()
![]() ,只有当
,只有当![]() ,
,
即![]() 时,等号成立
时,等号成立
∴S≥2×6+12=24,
∴S四边形ABCD有最小值24.
此时,P(3,4),C(3,0),D(0,4),AB=BC=CD=DA=5
∴四边形ABCD是菱形.


科目:初中数学 来源: 题型:
【题目】甲、乙两所医院分别有一男一女共4名医护人员支援湖北武汉抗击疫情.
(1)若从甲、乙两医院支援的医护人员中分别随机选1名,则所选的2名医护人员性别相同的概率是 ;
(2)若从支援的4名医护人员中随机选2名,用列表或画树状图的方法求出这2名医护人员来自同一所医院的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
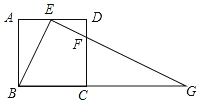
【题目】如图,在正方形ABCD中,E、F分别是边AD、CD上的点,AE=ED,DC=4DF,连接EF并延长交BC的延长线于点G.
(1)求证:△ABE∽△DEF;
(2)若正方形的边长为16,求BG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校运动会的立定跳远和1分钟跳绳两个单项比赛分成预赛和决赛两个阶段.下表为参加这两项比赛的10名学生的预赛成绩:
学生编号 成绩 项目 | 3104 | 3508 | 3115 | 3406 | 3317 | 3413 | 3218 | 3307 | 3519 | 3210 |
立定跳远(单位:米) | 1.96 | 1.92 | 1.82 | 1.80 | 1.78 | 1.76 | 1.74 | 1.72 | 1.68 | 1.60 |
1分钟跳绳(单位:次) | 163 |
| 175 | 160 | 163 | 172 | 170 |
|
| 165 |
在这10名学生中,同时进入两项决赛的只有6人,进入立定跳远决赛的有8![]() 的值是__________.
的值是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
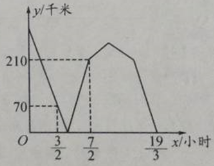
【题目】一辆快车从甲地出发到乙地,一辆慢车从乙地出发到甲地,两车同时出发,匀速行驶,慢车到甲地后停止行驶,快车到乙地后休息半小时,然后以另一速度返回甲地.两车之间的距离![]() (千米)与快车行驶的时间
(千米)与快车行驶的时间![]() (小时)之间的函数关系,如图所示.当慢车到达甲地时,快车与乙地的距离为_____千米.
(小时)之间的函数关系,如图所示.当慢车到达甲地时,快车与乙地的距离为_____千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
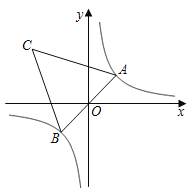
【题目】如图,在反比例函数![]() 的图象上有一动点
的图象上有一动点![]() ,连接
,连接![]() 并延长交图象的另一支于点
并延长交图象的另一支于点![]() ,在第二象限内有一点
,在第二象限内有一点![]() ,满足
,满足![]() ,当点
,当点![]() 运动时,点
运动时,点![]() 始终在函数
始终在函数![]() 的图象上运动,若
的图象上运动,若![]() ,则
,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰Rt△ABC和⊙O如图放置,已知AB=BC=1,∠ABC=90°,⊙O的半径为1,圆心O与直线AB的距离为5.
(1)若△ABC以每秒2个单位的速度向右移动,⊙O不动,则经过多少时间△ABC的边与圆第一次相切?
(2)若两个图形同时向右移动,△ABC的速度为每秒2个单位,⊙O的速度为每秒1个单位,则经过多少时间△ABC的边与圆第一次相切?
(3)若两个图形同时向右移动,△ABC的速度为每秒2个单位,⊙O的速度为每秒1个单位,同时△ABC的边长AB、BC都以每秒0.5个单位沿BA、BC方向增大.△ABC的边与圆第一次相切时,点B运动了多少距离?

查看答案和解析>>
科目:初中数学 来源: 题型:
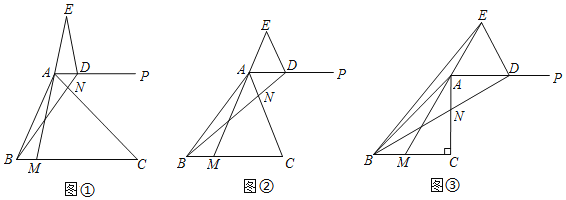
【题目】在△ABC中,CA=CB,0°<∠C≤90°.过点A作射线AP∥BC,点M、N分别在边BC、AC上(点M、N不与所在线段端点重合),且BM=AN,连结BN并延长交AP于点D,连结MA并延长交AD的垂直平分线于点E,连结ED.
(猜想)如图①,当∠C=45°时,可证△BCN≌△ACM,从而得出∠CBN=∠CAM,进而得出∠BDE的大小为 度.
(探究)如图②,若∠C=α.
(1)求证:△BCN≌△ACM.
(2)∠BDE的大小为 度(用含a的代数式表示).
(应用)如图③,当∠C=90°时,连结BE.若BC=3,∠BAM=15°,则△BDE的面积为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com